| |
SOLAR RADIATION AND CLIMATE
OF THE EARTH |
|
FLUCTUATIONS OF SOLAR CLIMATE AS THE BASIS OF REMODELING, ANALYSIS AND PREDICTION OF CHANGES IN GLOBAL CLIMATE OF EARTH V.M.
Fedorov Herein we give a brief overview of Earth’s solar climate research as the basis for remodeling, analysis and prediction of changes in global climate. We consider results of solar climate variability based on calculations of incoming solar radiation inclusive of ellipticity, axis and perihelion longitude secular drift. We give results of Earth solar climate space-time variability research with consideration of its orbital motion periodical perturbations and axis inclination.
Secular Variability of Solar Climate Secular fluctuations of solar radiation, connected with celestial and mechanic processes are determined by calculation methods. Such astronomic elements, subject to secular perturbations, as perihelion longitude, ellipticity and Earth axis inclination, which have quite prolonged periods of fluctuations are considered in the studying of secular fluctuations of solar stream (Milankovich, 1939; Sharaf, Budnikova, 1967, 1968, Berger, 1978 а, 1978 b, 1981). History of studying solar energy secular fluctuations, determined by celestial and mechanical processes reflects development of studies relating to astronomic theory of climate (Khrgian, 1986; Drozdov, etc. 1989; Monin, Shishkov, 1978, 2000; Monin, 1982; Imbrie, 1982; Imbrie et al., 1993; Melnikov, Smulsky, 2009; Smulsky, 2013; Vakulenko, etc., 2003; Vakulenko, etc. 2007). Introduction of astronomic theory of climate was preceded by development of concepts about distribution of inland ices during history of the Earth. Astronomic theory of climate emerged as a need to explain and physically substantiate glacier theory. Astronomic theory of climate origin refers to the middle of the 19th century and was connected with works of J. Adhemar, where he formulated a vision that a basic reason for ancient glaciations could be irregularities in characteristic pace of the Earth revolution around the Sun (Adhemar, 1842). According to Adhemar, glacial climates were a function of 22,000 year precession cycle, where glaciations took place successively every 11,000 years, blanketing one hemisphere after another – depending on which of them a period of prolonged winter seasons fell (winter season aligned with position of Earth near aphelion). Fundamental idea of J. Adhemar about successive heating up and cooling down of Northern and Southern hemisphere of Earth was questioned by a German naturalist A. Humboldt and English astronomer J. Herschel. A. Humboldt, for example, has fairly noticed that average temperature of any hemisphere is determined not by a number of hours (days) of warm and cold seasons, but by quantity of solar energy calories which it obtains during the year (Humboldt, 1866). However, hypothesis of J. Adhemar about relation of climatic changes to specific astronomic phenomena (precession of equinoxes) has become a basis for further development of notions about astronomic factors of climate fluctuation (Milankovich, 1939; Berger, 1988; Imbrie, Imbrie, 1988; Imbrie, 1982; Imbrie et al., 1993; Bolshakov. 2003; Bolshakov, Kapitsa, 2011). Notions about connection between ancient glaciations periods and astronomic mechanisms have been developed in works of a Scottish scientist J. Croll (Croll, 1875; Milankovich, 1939; Schwarzbach, 1955). Variability in Earth orbit ellipticity is assumed in ideas of J. Croll as a foundational astronomic factor (together with precession cycle). Using formulas of U. Leverrier (Leverrier, 1855, 1856) J. Croll calculated ellipticity of Earth orbit for a number of points for the last three million years (where he considered seven planets known at that time). In effect of calculations made, he designated cyclical pattern of ellipticity fluctuations. Analyzing the obtained data J. Croll arrived at hypothesis that reason for glacial epochs may be connected with conditions of mostly elongated orbit. From U. Leverrier’s works it follows that total volume of energy obtained by Earth during the year has almost no influence on variations of ellipticity of its orbit. However, Croll demonstrated, that coupled with Earth reflectivity (albedo), intensity of radiation arriving to Earth during astronomic semesters considerably depends on ellipticity fluctuation. As a result, J. Croll offered a theory, which explained global climate changes (glacial and interglacial epochs), the basis of which were seasonal effects of Earth orbit ellipticity changes, of albedo and positive reactions influence (Croll, 1875; Milankovich. 1920; Milankovich, 1939; Markov, 1960; Imbrie, 1982; Imbrie et al., 1993; Bolshakov, 2003; Bolshakov, Kapitsa, 2011). Notions of J. Croll based on two astronomic factors—precession cycle and Earth orbit shape periodic change—were published in “Philosophical Magazine” in 1864. Secular oscillations in solar radiation arriving to Earth were discussed in works of L. Meech (Meech, 1856). He arrived at formulas, which connect arriving radiation (for any latitude) with ellipticity, perihelion longitude and obliquity of ecliptic secular oscillations. R. Ball (Ball, 1891), imparted mathematic form to J. Croll’s theory with allowance for two parameters: ellipticity and precession. In which case, as influence on total volume of solar energy, obtained by separate hemispheres, a third astronomic factor which was considered was obliquity of ecliptic. Works of E. Culverwell (Culverwell, 1894, 1895), R. Hargreaves (Hargreaves, 1896), N. Ekholm (Ekholm, 1901) also refer to development of astronomic theory, but mathematical part of the problem was investigated in detail in works of M. Milankovich (Croll, 1875; Milankovich, 1920; Milankovich, 1939; Schwarzbach, 1955; Markov, 1960; Monin, Shishkov, 1979; Monin, 1982; Bolshakov, Kapitsa, 2011). Thus, until the end of the 19th century it was known, that distribution of insolation over the surface depends on three orbital characteristics: orbit ellipticity, Earth axis inclination and position of equinoxes points in its precession cycle. Works of a German mathematician L. Pilgrim appeared at the beginning of the 20th century, where the results of new calculations of these astronomic characteristics were stated (“Experience of numeric development of glacial periods problem development”) for the time period of 1010 millenia up to 1850 AD. (Pilgrim, 1904). Consequently, calculation of arriving solar energy became principally possible. Calculations of secular changes in astronomic elements by L. Pilgrim (for 600,000 years), were recalculated by V. Miskovic (director of astronomic observatory in Belgrade). These data became a basis for calculations by M. Milankovich of solar insolation secular fluctuations. In his calculations V. Miskovic proceeded from calculations of orbital characteristics and planets mass, produced by U. Leverrier. L. Pilgrim used data of J. Stockwell (Stockwell, 1872) inferior in accuracy to calculations of U. Leverrier. Accuracy in calculations of V. Miskovic was: for ellipticity – up to four decimal digits, for obliquity of ecliptic – up to seconds, for perihelion longitude – up to minutes for a time period, at least, 100,000 years before and after contemporary epoch (beginning of 1800). Though, it is worth noting that at that time S. Newcomb (Newcomb, 1895) drew up extremely accurate tables of planetary motion (considering Uranus, Neptun and some satellites of planets), which were used in astronomy up to the middle of the 20th century, however, for some reasons, M. Milankovich didn’t use them in his calculations. Calculations of U. Leverrier were based on secular perturbations, calculated by J. Lagrange (Lagrange, 1781). Values of planets mass and those digital data, which J. Lagrange used for initial conditions acquisition were not accurate enough (M. Milankovich also noted that). From nine planets known to that moment J. Lagrange could assume only six. Uranus was discovered (by J. Herschel in 1781) when J. Lagrange made his calculations and elements of this new planet were not determined even approximately. Nothing was known about its satellites. Neptun was discovered (based on calculations of U. Leverrier, connected with perturbation in orbital motion of Uranus) only in 1846. Mars was considered as having no satellites. That is why the determination of two planets mass (Mars, Uranus) J. Lagrange could only base on dactylic data. Nevertheless, he managed, though approximately, to determine outlines, within which planets orbits ellipticities, inclination of their orbits planes and obliquity of ecliptic could change. Within the context of this overview, the conclusion that semi major axes of orbits do not undergo secular drifts, obtained by J. Lagrange appears essential and was later included by P. Laplace into Solar System Stability Theory (Laplace, 1825; Arnold, 1963; Duboshin, 1975, 1978; Laplace. 1982). M. Milankovich determined climatic effects of secular fluctuations in three astronomic elements: obliquity of ecliptic (ε), ellipticity (e) and perihelion longitude (П). Thus, increase of Earth axis inclination (relative to perpendicular to ecliptic plane) results in reduction of annular volume of radiation in equatorial area and its increase in polar areas, i.e. leveling of distinctions between equatorial and polar areas takes place. Decrease of inclination leads to opposite results, intensifying latitudinal contrasts in distribution of solar radiation over Earth surface (in the absence of atmosphere). At ε = 0, when both poles during the year remain unlighted, latitudinal contrasts are maximal (Milankovich, 1939). Axis inclination changes have relatively regular oscillating character with average period of about 40,000 years. During that period latitudinal differences achieve maximum one time (at the least obliquity of ecliptic), in which case, seasonal differences at that time achieve their minimum, and one time, in 20,000 years—their minimum (at maximum obliquity), when seasonal differences are mostly expressed. These phenomena could repeat periodically, if only they were not overlapped by influences of other astronomic elements (Milankovich, 1939). Annual course of solar radiation is also determined by duration of summer and winter seasons (semesters), which is a function of two elements of Earth orbit—ellipticity (е) and perihelion longitude (П). Owing to variability of both elements е and П difference in arrival of radiation between summer and winter seasons (semesters) is a function of time. In such a way, perihelion longitude, during about 21,000 years, increases almost evenly for 360° , since perihelion during that time, with almost even speed, traces a full cycle. Ellipticity value (е) also undergoes oscillations with period of 92,000 years (with considerably smaller amplitude), remaining embosomed between 0 and 0.0677. Fluctuations of difference in duration of summer and winter seasons depend on both factors, but influence of the first one is considerably stronger. Consequently the value of difference (between arrival in summer and winter time) fluctuates about some average value with period of 21,000 years, and variability of all these oscillations amplitude is characterized by a period of about 46,000 years (Milankovich, 1939).
As perihelion longitude increases from 0° to 90° duration of summer semester in the Northern hemisphere increases, and decreases for winter semester. According to this, intensity of solar radiation in summer period decreases and in winter increases. At perihelion longitude equal to 90° (perihelion matches with winter solstitial point), duration of summer semester in Northern hemisphere achieves its maximum, and average intensity of radiation reduces in summer to minimum, and becomes maximum in winter. Thus, seasonal contrasts in this period of time are minimal. This is true, but only for Northern hemisphere. In Southern hemisphere duration of summer semester (matches with winter semester in Northern hemisphere) reduces, while quantity of radiation, obtained by Southern hemisphere during such short summer equals to the quantity which arrives at Northern hemisphere during its summer, which is longer. That is why in Southern hemisphere summer semester is shorter during this period of time and is characterized by higher intensity of incoming solar radiation, and longer winter semester by lower intensity. Consequently, seasonal differences in Southern hemisphere at this period of time are maximal (as opposed to Northern hemisphere). At perihelion longitude equal to 180° (perihelion matches with fall equinox point) summer and winter semester have equal duration in both hemispheres. Quantities of solar energy incoming during semesters are equal, both for semesters and for hemispheres. Latitudinal differences in radiation incoming to outer fringe in such cases are maximal. At perihelion longitude equal to 270° (perihelion matches with summer solstitial point) duration of summer semester in Northern hemisphere is minimal and contrast between summer and winter seasons (semesters) is mostly sharp. In Southern hemisphere for this longitude of perihelion there is an opposite situation – prolonged summer season (with lower intensity of incoming radiation) and shorter winter season (with higher intensity of incoming radiation). Seasonal contrasts in this case become leveled. Thus, latitudinal differences are maximal when perihelion is in equinoxial points and leveled when perihelion is in solstitial points. In this case, if perihelion is in winter solstitial point, seasonal differences in Northern hemisphere are mostly contrasted and in Southern hemisphere they are leveled. When perihelion is in summer solstitial point the situation becomes reverse. In this case, seasonal contrasts become maximally expressed in Southern hemisphere and leveled in Northern hemisphere (Milankovich, 1939; Monin, Shishkov, 1979; Imbrie, 1982; Imbrie, Imbrie, 1988; Bolshakov, 2003).
Instead of calculation of heat quantities
during summer and winter semesters M. Milankovich used caloric semesters.
Caloric semesters are determined as semesters of equal duration
Detailed calculations were held by Soviet astronomers S. G. Sharaf and N.A. Budnikova (Sharaf, Budnikova, 1967, 1968, 1969). They found out mistakes in initial values of Venus and Earth nodes, used by D. Brouwer and A. Van Woerkom. Based on amended values of S.G. Sharaf and N.A. Budnikova there were integration constants recalculated and trigonometric formulas developed for precession and axis inclination, which included second-order terms for ellipticity and inclination. As a result, they calculated fluctuations of insolation for a period of 30 mln. years in the past and of 1 mln. years in the future. It turned out, that values of ellipticity fluctuated within the limits 0.0007-0.0658 (at present 0.01675), preferably with periods about 0.1; 0.425 and 1.2 mln. years. Variations of axis inclination value took place with periods of about 41 and 200 thousand years and were determined by limits from 22.068° to 24.568° . Declines of values е • sin П from its value in 1950 fluctuated between +0.03 and -0.07 with average period of about 21 thousand years. Variations of equivalent latitudes were determined by limits between 58°-79° (quite considerable) with predominant periods of 41 thousand years and 1.2 mln. years. Equivalent latitudes trend graphics, made by S.G. Sharaf and N.A. Budnikova are given in fig. 3. By means of axis inclinations, ellipticity and perihelion longitude values, obtained by S.G. Sharaf and N.A. Budnikova in the Oceanology Institute of Russian Academy of Scientists insolation values were calculated for million years into the past and future in relation to contemporary epoch with time increments of 5 thousand years and latitude increments of 10 (Monin, 1982; Monin, Shishkov, 2000). Total radiation for caloric semesters was calculated based on relation:
where I0 is solar constant (equal to 2 cal/min • cm2), T0 – duration of tropical year (accepted as constant), S – functions, describing distribution of annual insolation along a meridian, φ - geographic latitude, П – perihelion latitude, e – ellipticity, ε - obliquity of ecliptic. From formula (1) it is seen, that values QS,W depend on axis inclination ε and from elements of Earth orbit r0(via I0 and T0), e and П (Monin, 1982). Calculations with the use of formula (1) indicated, that insolation anomalies during caloric semesters are maximal within summer polar areas, where they achieve values of ±250 MJ/m2, and in general reduce towards winter polar areas. It is noted, that variation of anomalies has quasi-periodical character with a period of about 40.000 years (Vulis, Monin, 1979; Monin, 1982; Monin, Shishkov, 2000). Again, calculations of secular variations of Earth orbit elements and insolation were made by A. Vernekar (Vernekar, 1972), P. Bretagnon (Bretagnon, 1974). Later, A. Berger (Berger, 1978 а) offered an improvement for D. Brouwer and A. Van Woerkom’s solution (having included third-order terms for ellipticity and axis inclination) and calculated fluctuations of orbit and insolation elements. Comparison of calculated fluctuations of solar radiation is given in fig. 3. From graphics presented, it is seen that the last maximum in arriving solar radiation for Northern hemisphere was noted about 10 thousand years ago (corresponds to general notions about inland ice degradation time in Europe and North America). From that time, gradual reduction of incoming solar radiation takes place, which, according to calculations of S.G. Sharaf and N.A. Budnikova, will continue for about 10 thousand years more (Sharaf, Budnikova, 1969). It should be noted, that for approximate analytical problem solving connected with orbital motion, physical and mathematical simplifications are introduced (e.g., interrelating bodies are considered as material points or bodies with specific shape, etc.). Thereby, possible mistakes in calculations for large periods tend to escalate (for this reason, M. Milankovich supposed that reliable results may be obtained for a period of 600 thousand years). S.G. Sharaf and N.A. Budnikova clarified initial data and precession solutions, and calculated insolation for an interval of 30 mln. years. A. Berger and M. Loutre made calculations for an interval of 5 and 3 mln. years (Berger, Loutre 1991, 1992), T. Quinn with colleagues calculated fluctuation of insolation for 3 mln. years (Quinn et al., 1991). J. Laskar and colleagues improved the theory of secular perturbations and made calculations of insolation change for a period of time up to 200 mln. years, but for reasons of chaotic character effects in behavior of basic characteristics, they came to a conclusion that results may be deemed authentic only within the period from 20 mln. years in the past and up to 10 mln. years in the future (Laskar, 1988; Laskar et al., 1993, 2004). On the whole, history of astronomic theory of climate is connected with acquisition of a series of calculated values for secular fluctuations of incoming solar radiation (Earth solar climate) connected with secular fluctuations of Earth orbit elements (ellipticity, perihelion longitude) and axis inclination. Quantitative results for this solution—calculation of solar radiation secular fluctuations—are somewhat different because of the discrepancies in initial conditions and in methods of calculations (fig. 3.). Univalent solution for the problem of global climatic changes (development of glaciations) from a perspective of astronomic theory of climate was not obtained. Correlation search of connection of extreme values periods in radiation arrival with periods of maximum glaciations development and with interglacial periods without consideration of atmosphere, ocean and other factors affecting the formation of global climate turned out to be non-efficient in relation to search of reasons for its changes (Schwarzbach. 1955; Kukla, 1975). A number of other phenomena, e.g. glaciations metachronousity, complexifies explanation for development of glaciations by secular fluctuations of solar radiation (Kolosov. 1947; Markov, 1960), absence of glaciations during long lasting geological periods (e.g., Cretaceous period). Thus, in scale of geological time other (except for solar climate) climate forming factors may become acute, e.g. fluctuation in Earth rotational rate, continents movement, polar motion, fluctuation of relief, continents and oceans configuration, their squares, change in ocean currents course, atmosphere composition and atmospheric circulation character, volcanic activity, etc. (Вегенер, 1925; Koppen, Wegener, 1924; Такеучи и др., 1970; Ле Пишон и др.. 1977; Уеда, 1980; Ушаков, Ясаманов, 1984) Solar climate fluctuations seem to be of a higher priority factor in climate forming in the process of climatic changes analysis at short time intervals. Chaotic motions of, for example rotation axis, are also considered as mechanisms, which intensify solar climate variability factor in its impact on global climate (Laskar, 1990, 2004; Laskar, Robutel, 1993; Prigozhin, Stengers, 2003; Resonances in celestial mechanics, 2006). At the end of the past century, explanations of global climatic changes (genesis of glacial and inter-glacial epochs) appeared in geological past of our planet, the basis of which is an effect of stochastic resonance—response of bistable or metastable nonlinear system to a weak periodic signal at noise impact of specific energy (Berger, 1981; Nicolis, 1981, 1982, 1993; Nicolis, Prigogina, 1989; Baker, Gollub, 1990; Anischenko, etc., 1999, 2006). However, these ideas are not completely accepted yet by geophysics and palaeoclimatologists. Finally, it is a reminder that time range of research relating to astronomic theory of climate, shall be determined by study of solar radiation secular fluctuations, which is connected with the basic problem of explanation of global climatic events through geological time. In astronomic theory of climate solar radiation secular fluctuations shall be calculated in connection with secular perturbations of two orbital elements: orbit ellipticity and perihelion longitude, as well as axis inclination. In such a case, it is thought that “Perturbations may be of two types: periodic, taking place in extremely narrow limits and secular. The first almost do not have any influence on irradiation of Earth and thus are of no interest to us” (Milankovich, 1939). Calculations made by M. Milankovich show, that “radiation quantities, obtained during astronomic spring and summer, are equal as radiation quantities during fall and winter.” Also it follows from calculations that “any latitude of Southern hemisphere obtains during its summer semester the same quantity of radiation, as the same latitude of Northern hemisphere during its summer semester; the same refers to winter semesters” (Milankovich, 1939). In the process of studying secular fluctuations we assume constancy of both Earth orbit major semiaxis (according to Laplace’s stability theorem) and duration of Earth revolution time around the axis (according to Kepler third law) (Milankovich, 1939). It should also be reminded that Kepler laws are true for unperturbed motion. All calculations for incoming solar radiation which were mentioned above, are united by one thing: they were held for long-term time intervals. That is why they do not consider periodic perturbations and Earth orbital motion fluctuations connected with them and its axis inclination. As it was truly mentioned by J. Lagrange, P. Laplace and M. Milankovich, periodic perturbations are not essential compared to secular perturbations when considering Earth solar climate through geological time. Although, for study of solar climate within short-term time intervals (within contemporary epoch) consideration must be given to incoming solar radiation fluctuations with account for periodic perturbations of Earth orbital motion and its axis inclination. Specifically for short-term interval (decades, centuries), fluctuations of Earth solar climate may have crucial importance among other reasons for global climate variation. Weather conditions fluctuations are studied within even shorter time frame (hours – days – months).
Periodic Perturbations Time frame of our studies allows taking into account small fluctuations of solar radiation, connected with celestial and mechanic processes, periodic perturbations of Earth orbital motion (Fyodorov. 2012, 2013, 2014). It should be noted that Laplace’s theorem is true only in the absence of comparabilities in mean motion of major planets (Arnold, 1963; Duboshin, 1975, 1978). However, in mean motion of Earth and nearest planets (Mars, Venus and Jupiter) (Grebennikov, Ryabov, 1978) we can distinguish comparabilities (2/1, 3/5, 12/1 accordingly) or phenomenon of orbital resonance. For that reason, constancy of Earth orbit major semiaxis and its revolution period duration around the Sun are not really carefully followed. Periodic small fluctuations of Earth solar climate are connected with periodic fluctuations of Earth orbit major semiaxis size, duration period of its revolution around the Sun and axis inclination, due to orbital resonance (Fyodorov, 2012, 2013, 2014). As it appears from a brief historic overview, necessity of new calculations and new approach to search of solar radiation fluctuations connection with global climate change is determined by at least two main reasons. First, it is connected with constant update of initial data for calculations which account for changes in theory of perturbations. At present time such data are presented, for example in astronomical ephemerides (JPL Planetary and Lunar Ephemerides). Second, Earth climatic system response within temporal range of secular fluctuations is not expressly specified. This results in the need for a new approach in search of solutions to a problem of climatic changes relation to solar radiation fluctuations—of solar radiation calculations based on new initial data within fluctuations periodic range (i.e. within another time format, with another time resolution, within another time frame). Subject matter of our research is identifying a relation between variations in Earth climatic system and its components with solar radiation fluctuations (inclusive of periodic perturbations and minor fluctuations of solar climate) within a small dimension time interval.
Research of Earth solar climate fluctuations within a periodic range appear to be promising for a number of reasons:
1) This time dimension is provided with astronomic data most accurate at present day. Our calculations are based on astronomic data on celestial bodies motion (JPL Planetary and Lunar Ephemerides DE-405/406), calculated for time interval from 3000 B.C. till 3000 A.D. 2) This time range is mostly provided with detailed climatological information, which allows to perform detailed research of relation of climatic elements fluctuations and variability of solar radiation arriving to Earth (determination of climatic system sensitivity to solar radiation fluctuations). 3) Calculations of incoming radiation refer to astronomical seasons, semesters and tropical years real in duration (but not to conventional caloric semesters), which allows to obtain a more sound and real picture of spatial and temporal variability of Earth solar climate. 4) Selected time scale is convenient for comparison of fluctuations having different physical nature (celestial and mechanic processes and Sun activity) and allows to get a complete physical picture of fluctuations in intensity of solar radiation incoming to the Earth.
Calculations of incoming solar radiation within a range of periodic perturbations were initiated in Main Geophysical Observatory named after A.I. Voyeykov (Borisenkov, Tsvetkov, Agaponov, 1983; Borisenkov, Tsvetkov, Eddy, 1985). Astronomical ephemerides of S. Newcomb were used in this case and since 1987, ephemerides of the Institute of Applied Astronomy of Russian Academy of Sciences. However, this research has not got any further development. The results of new calculations of solar radiation within the periodic range are presented in a corresponding section of the website.
|
|
SOLAR RADIATION AND CLIMATE |
||
|
© www.solar-climate.com
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|||
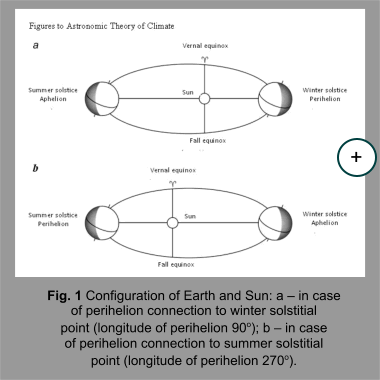 Dependence of secular trend of arriving radiation from changes in perihelion
longitude (orbit perihelion longitude—angle between direction from the
Sun to perihelion and vernal equinox point presently equals to 102°
08), is expressed in the following way. Difference in duration of summer
and winter semesters equals to 0, only if perihelion longitude equals
to 0° (perihelion matches with vernal equinox point) and to 180°
(perihelion matches with fall equinox point). In which case, quantities
of solar radiation arriving during semesters equal both for semesters
and for hemispheres. Latitudinal differences in radiation arriving to
Earth outer fringe are maximal in these cases (fig. 1).
Dependence of secular trend of arriving radiation from changes in perihelion
longitude (orbit perihelion longitude—angle between direction from the
Sun to perihelion and vernal equinox point presently equals to 102°
08), is expressed in the following way. Difference in duration of summer
and winter semesters equals to 0, only if perihelion longitude equals
to 0° (perihelion matches with vernal equinox point) and to 180°
(perihelion matches with fall equinox point). In which case, quantities
of solar radiation arriving during semesters equal both for semesters
and for hemispheres. Latitudinal differences in radiation arriving to
Earth outer fringe are maximal in these cases (fig. 1).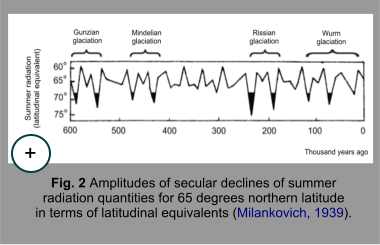 Based on calculations of astronomic elements secular drift (made by
V. Miskovic), M. Milankovich calculated values of insolation for 65-degree
parallel of Northern hemisphere for the last 650,000 years. Graphic
of insolation obtained by Milankovich (in values of latitudinal equivalents)
was for the first time published in 1924 in the work of V. Koppen and
A. Wegener (Koppen, Wegener, 1924) “Climates
of the Past” (fig.2). Latitudes equivalent for the 65° of Northern
latitude are the latitudes at which at present during summer caloric
semester the same quantity of solar radiation arrives, as in the past
arrived at latitude of 65° of Northern latitude. Increase of equivalent
latitude means reduction of incoming radiation and vice versa (e.g.,
solar radiation incoming to the Earth at 65° of Northern latitude
590,000 years ago, is characteristic for latitude at 72° of Northern
latitude in 1800s).
Based on calculations of astronomic elements secular drift (made by
V. Miskovic), M. Milankovich calculated values of insolation for 65-degree
parallel of Northern hemisphere for the last 650,000 years. Graphic
of insolation obtained by Milankovich (in values of latitudinal equivalents)
was for the first time published in 1924 in the work of V. Koppen and
A. Wegener (Koppen, Wegener, 1924) “Climates
of the Past” (fig.2). Latitudes equivalent for the 65° of Northern
latitude are the latitudes at which at present during summer caloric
semester the same quantity of solar radiation arrives, as in the past
arrived at latitude of 65° of Northern latitude. Increase of equivalent
latitude means reduction of incoming radiation and vice versa (e.g.,
solar radiation incoming to the Earth at 65° of Northern latitude
590,000 years ago, is characteristic for latitude at 72° of Northern
latitude in 1800s).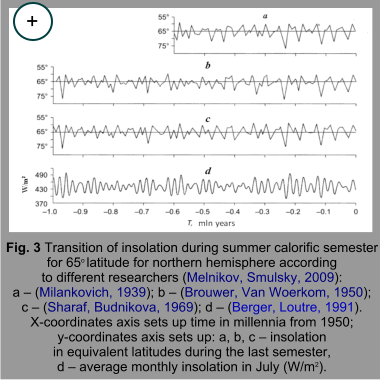 Calculations made by M. Milankovich were further made with adjustments
by a number of authors. These calculations based on new solutions of
secular perturbations theory obtained for the whole Solar system in
1950 by D. Brouwer and A. Van Woerkom (Brouwer,
Van Woerkom, 1950). Calculations involved the newest data about
mass and motion of planets, considered second order effects, caused,
for example, by long-period inequalities within Jupiter and Saturn motion.
Calculations made by M. Milankovich were further made with adjustments
by a number of authors. These calculations based on new solutions of
secular perturbations theory obtained for the whole Solar system in
1950 by D. Brouwer and A. Van Woerkom (Brouwer,
Van Woerkom, 1950). Calculations involved the newest data about
mass and motion of planets, considered second order effects, caused,
for example, by long-period inequalities within Jupiter and Saturn motion.



