| |
СОЛНЕЧНАЯ РАДИАЦИЯ И КЛИМАТ ЗЕМЛИ СОЛЯРНАЯ ТЕОРИЯ ИЗМЕНЕНИЙ
КЛИМАТА |
Препринт статьи принятой в журнал «Криосфера Земли» http://www.izdatgeo.ru/index.php?action=journal&id=2
ПРОГНОЗ ИЗМЕНЕНИЯ СУММАРНОГО БАЛАНСА МАССЫ ЛЬДА В ЛЕДНИКОВЫХ РАЙОНАХ СЕВЕРНОГО ПОЛУШАРИЯ В.М. Федоров Московский
государственный университет имени М.В. Ломоносова Проведен корреляционный анализ регионально осредненных рядов суммарного баланса массы льда 9-ти ледниковых районов Северного полушария с инсоляционной контрастностью. Определено, что изменчивость суммарного баланса массы в исходных данных на 90 – 97% учитывается трендом. На основе найденной корреляционной связи получены линейные и полиномиальные уравнения регрессии. По ансамблю линейных и полиномиальных решений выполнен прогноз изменения регионально осредненного суммарного баланса массы льда до 2050 г. В полученных уравнениях регрессии дисперсия также на 90 – 97% определяется трендом инсоляционной контрастности, что позволяет сделать вывод о причинно-следственной связи деградации современного оледенения с тенденцией изменения инсоляционной контрастности. Тенденция в изменении инсоляционной контрастности, определяющей усиление работы «тепловой машины первого рода», связана с уменьшением угла наклона оси вращения Земли. Ключевые слова: баланс массы льда, ледниковые районы, инсоляция, межширотный теплообмен, регрессионная модель, прогноз. V.M. Fedorov THE
FORECAST OF CHANGES IN TOTAL MASS BALANCE OF ICE IN THE GLACIAL REGIONS
OF THE NORTHERN HEMISPHERE The сorrelation analysis between the regional averaged series of the total mass balance of the ice and insolational contrast performed for the nine glacial regions of the Northern Hemisphere. It is determined that the variability of the total mass balance in the original data by 90 - 97% described the trend. The linear and polynomial regression equations obtained on the basis of the found correlation. The forecast of changes in regional average total mass balance of the ice made on the basis of the ensemble of linear and polynomial solutions up to 2050. The dispersion in the obtained regression equations is also determined by the trend in insolational contrast at 90 – 97%. This allows to make a conclusion about the causal connection between the degradation of recent glaciation and trend in insolational contrast. The trend in the insolational contrast variations associated with a decrease of the angle of inclination of the Earth`s axis rotation. This trend defines the amplification of the "heat machine of the first kind". Key words: mass balance of the ice, glacial areas, insolation, inter-latitudinal heat transfer, regression model, forecast.
Введение Прогноз изменения баланса массы льда в ледниковых районах представляется актуальным, во-первых, в связи с тем, что ледники являются индикаторами региональных климатических изменений. Во-вторых, горные ледники являются одной из составляющих водных ресурсов, учет которых важен для определения стратегии социально-экономического развития регионов. Многолетние изменения массы льда в ледниковых районах Земли связаны, прежде всего, с изменением глобальной температуры являющейся одним из основных показателей изменяющегося климата. Главным источником тепла на Земле является приходящая от Солнца лучистая энергия. В перераспределении приходящей к Земле энергии участвуют механизмы теплообмена, важнейшими из которых (Шулейкин, 1953) является межширотный теплообмен («тепловая машина первого рода») и теплообмен между океаном и материками («тепловая машина второго рода»). Перенос тепла к климатической системе Земли связан с циркуляционными процессами в атмосфере и океане. Циркуляционные процессы в атмосфере вносят существенные изменения в годовой, сезонный и суточный ход изменения температуры воздуха, который определяется, поступающей от Солнца энергией. Они существенно деформируют, связанную с приходящей солнечной радиацией суточную, сезонную и годовую периодичность в изменении температурного режима. С циркуляционными процессами в атмосфере связано образование и распространение атмосферных осадков. Таким образом, циркуляционные процессы влияют на ход основных климатических показателей (элементов) определяющих условия развития ледников и в связи с этим представляются (наряду с приходящей от Солнца энергией), важнейшим фактором как распространения ледников в пространстве, так и их развития во времени. Таким образом, основными факторами развития ледников является приходящая от Солнца лучистая энергия и циркуляционные процессы в атмосфере определяющие перенос тепла и образование атмосферных осадков. При этом общая динамика циркуляционных процессов тесно связана с инсоляцией (Федоров, 2015 в; Федоров, Кононова, 2014). Несмотря на то, что астрономическая теория изменения климата, основу которой составляет расчет инсоляции Земли, создавалась для объяснения причин плейстоценовых материковых оледенений (Миланкович, 1939; Имбри, Имбри, 1988) связь динамики баланса массы ледников с инсоляцией Земли исследована не достаточно. Одной из сложностей исследования развития ледников в прошлом и прогноза их развития в будущем являются непродолжительные ряды исходных данных. В связи с этим одной из важнейших задач криолитологии и гляциологии является увеличение временных рядов инструментальных наблюдений (Серебрянный и др., 1979). Эта задача решается созданием гляциологических реконструкций. Реконструкция выполнялась автором на основе найденных связей динамики баланса массы ледников с продолжительностью макроциркуляционных процессов в атмосфере (Федоров, 2006, 2007, 2009 а, б, 2011 а, б). Прогнозы рассчитывались на основе найденной связи суммарного баланса массы льда в ледниковых районах с инсоляционной контрастностью (ИК).
Методика исследований В методике исследований для реконструкции суммарного баланса массы льда применялись расчеты весовых коэффициентов элементарных циркуляционных механизмов (ЭЦМ) с использованием типизации циркуляционных процессов в атмосфере (Федоров, 2011 б) и расчеты инсоляции Земли для выполнения прогнозов (Федоров, 2012, 2015 а, б, 2016 а, б).
Методика реконструкции баланса массы ледников Реконструкция суммарного баланса массы льда в ледниковых районах выполнялась на основе макроциркуляционных моделей. При этом использовалась типизация циркуляционных процессов в атмосфере, разработанная Б.Л. Дзердзеевским, В.М. Курганской и З.М. Витвицкой (Дзердзеевский и др., 1946) и Календарь последовательной смены ЭЦМ содержащий данные по циркуляции с 1900 г. по настоящее время (Кононова, 2003, 2009; http://www.atmospheric-circulation.ru). Схемы типизации атмосферных процессов представляют непрерывный процесс общей циркуляции атмосферы в виде чередования устойчивых многократно повторяющихся фрагментов – однородных процессов (охватывающих полушарие или значительные по площади регионы). Наибольшую известность в отечественной метеорологии получили типизации макромасштабных атмосферных процессов Г. Я. Вангенгейма – А.А. Гирса (Гирс, 1974) и Б.Л. Дзердзеевского, В.М. Курганской, З.М. Витвицкой (Дзердзеевский и др., 1946). В связи с четкостью формализации циркуляционных ситуаций, широкой пространственной и временной информативностью (разработана для всего северного полушария, охватывает период с 1899 года по настоящее время), общей доступностью Календаря последовательной смены элементарных циркуляционных механизмов (ЭЦМ) (Кононова, 2003, 2009, http://www.atmospheric-circulation.ru, для выполнения реконструкции суммарного баланса льда нами использовалась типизация Б.Л. Дзердзеевского, В.М. Курганской, З.М. Витвицкой. В качестве профилирующего признака в этой типизации принято соотношение зональной и меридиональной составляющих циркуляции над полушарием. Это соотношение в основном регулируется приходящей к Земле солнечной радиацией (Федоров, Кононова, 2014). Выделяется 13 основных типов элементарных циркуляционных механизмов (ЭЦМ), а с учетом их разновидностей (выделяемых на основе сезонных или региональных различий) – 41 ЭЦМ. ЭЦМ – представляет собой единый целостный макропроцесс, в течение которого в Северном полушарии сохраняется географическое распределение барического поля определенного типа и направленность основных переносов воздушных масс. По характеру соотношения зонального и меридионального переносов в северном полушарии ЭЦМ объединены в четыре группы: зональную, нарушения зональности, меридиональную северную и меридиональную южную. Группы зональная и нарушения зональности отражают зональный перенос в атмосфере, группы меридиональная южная и меридиональная северная – меридиональный перенос воздушных масс. Таким образом, в непрерывном циркуляционном процессе в атмосфере выделяются элементарные циркуляционные механизмы, группы циркуляции и циркуляционные сезоны, являющиеся основными структурными элементами рассматриваемой типизации. Время, частота, порядок проявления и продолжительность действия тех или иных ЭЦМ отражают особенности общей циркуляции атмосферы, определяют характер погоды каждого конкретного места. Продолжительность действия групп циркуляции, характер соотношения зональных и меридиональных форм циркуляции являются важнейшими макроциркуляционными характеристиками климата при рассмотрении его многолетних изменений. Применение типизации к анализу балансовых показателей ледников позволило разработать методику реконструкции баланса массы и увеличить продолжительность балансовых рядов. Основу методики реконструкции составили представления о расчете весовых коэффициентов каждого ЭЦМ в процессах аккумуляции и абляции на леднике, охваченном балансовыми наблюдениями (Федоров, 2011 б). Связь циркуляционных характеристик климата находилась из предположения о том, что каждому элементарному циркуляционному процессу на полушарии соответствуют определенные погодные условия в конкретном месте (температурный режим и режим атмосферных осадков), которые определяют развитие ледников. Связь циркуляционных характеристик (продолжительность действия ЭЦМ) с балансовыми показателями была найдена в виде пропорции циркуляционного вклада (весовых соотношений) каждого ЭЦМ в формирование знака и величины аномалии балансового показателя (Федоров, 2012, 2015 а, б, 2016 а, б). Пропорция вклада (весов) для рядов инструментальных наблюдений аккумуляции и абляции определялась следующим образом. Из ряда значений балансового показателя вычиталось среднее многолетнее значение. В результате была получена знакопеременная функция – аномалия балансового показателя (аккумуляции, абляции). Далее, по данным Календаря последовательной смены ЭЦМ (Федоров, 2011 б) для лет с положительными и отрицательными аномалиями отдельно находились суммарные значения продолжительности действия (в сутках) ЭЦМ всех типов за некоторый период года (например, зимний – для аккумуляции и летний – для абляции). Из предположения о том, что связанные с отдельными типами ЭЦМ погодные условия вносят определенный циркуляционный вклад в формирование как положительных, так и отрицательных аномалий годовых значений балансовых показателей ледника, были рассчитаны (в долях единицы) пропорции циркуляционного вклада (веса) каждого ЭЦМ в формирование знака и величины аномалии аккумуляции и абляции. Полученные пропорции проверялись восстановлением значений исходных инструментальных рядов по данным Календаря последовательной смены ЭЦМ (Федоров, 2011 б). В качестве оценочных характеристик при этом принимались коэффициент корреляции между восстановленным и исходным рядами и расхождение между этими рядами в миллиметрах водного эквивалента и в процентах от среднего модуля аномалии исходного ряда. Статистическая значимость коэффициента корреляции определялась в соответствии с существующими методиками (Цимбаленко и др., 2007). Изменением даты начала и продолжительности периода (аккумуляции, абляции) путем перебора находилось такое его значение, при котором величина коэффициента корреляции была максимальной, а расхождение – минимальным. Восстановленный ряд принимался за макроциркуляционную модель балансового показателя. На основе найденной формы связи были выполнены реконструкции динамики баланса массы 25-ти репрезентативных и опорных ледников Северного полушария, имеющих продолжительные ряды балансовых наблюдений (Федоров, 2011 а, б). Эти данные по районам были дополнены результатами балансовых наблюдений еще по 100 летникам Северного полушария. Затем рассчитывались регионально осредненные значения баланса массы для каждого района (по всем ледникам, охваченным балансовыми наблюдениями) и по ним значения суммарного баланса. Эти ряды использовались для прогнозов суммарного баланса массы льда в ледниковых районах Северного полушария.
Методика расчета инсоляции Расчеты приходящей на ВГА Земли солнечной радиации известны, начиная с работ М. Миланковича (Миланкович, 1939). Эти расчеты выполнялись, прежде всего, для объяснения плейстоценовых ледниковых эпох. Они проводились с учетом трех параметров орбитального движения Земли (эксцентриситет земной орбиты, наклон оси вращения Земли и долгота перигелия) на длительные периоды времени (сотни тыс. лет). Расчеты выполнялись только для отдельных широт. Принималось, что Земля имеет форму сферы. В расчетах, таким образом, принимались во внимание только вековые вариации характеристик орбитального движения Земли и, связанные с ними вариации в поступлении к Земле солнечной радиации. Периодические изменения элементов земной орбиты и наклона оси вращения Земли при этом не учитывались. Разрешение по времени в расчетах Миланковича и его последователей (Монин, 1982; Шараф, Будникова, 1969; Berger, 1978; Vernekar, 1972) составляло от 1 до 5 тысяч лет. Выполняемые таким способом расчеты могли быть полезными при анализе палеоклиматических изменений. Для анализа современного климата необходимы расчеты инсоляции с более высоким разрешением по времени, учитывающие наряду с вековыми и периодические вариации инсоляции. Такие расчеты, учитывающие периодические возмущения элементов земной орбиты и, связанных с ними высокочастотных вариаций солнечной радиации, были начаты в Главной геофизической обсерватории имени А.И. Воейкова, в России (бывшем СССР) (Borisenkov et al., 1983). Однако, дальнейшего развития эти исследования не получили. Исследования высокочастотных вариаций инсоляции также были начаты в бельгийском институте астрономии и геофизики имени Г. Леметра (Berger et al., 2010; Bertrand et al., 2002; Loutre et al., 1992). Расчеты инсоляции (на основе решения задачи о движении 2-х тел) в этом диапазоне также были выполнены в Институте криосферы Земли (Тюмень) И.И. Смульским и О.И. Кротовым (Смульский, Кротов, 2013). Позднее расчеты инсоляции в диапазоне высокочастотных вариаций были выполнены автором совместно с А.А. Костиным (http://www.solar-climate.com/sc/mtd.htm). Расчеты приходящей солнечной радиации выполнялись по данным астрономических эфемерид (Giorgini et al., 1996; http://ssd.jpl.nasa.gov) для всей поверхности Земли (без учета атмосферы) в интервале с 3000 г. до н.э. по 2999 г. н.э. Исходными астрономическими данными для расчетов инсоляции были склонение и эклиптическая долгота Солнца, расстояние от Земли до Солнца, разность хода равномерно текущего (среднего солнечного) и всемирного корректируемого времени (истинного солнечного). Поверхность Земли аппроксимировалась эллипсоидом (GRS80 – Geodetic Reference System, 1980) с длинами полуосей равными 6378137 м (большие) и 6356752 м (малая). В общем виде алгоритм расчетов можно представить выражением:
где I – приходящая солнечная
радиация за элементарный n-й фрагмент m-го тропического
года (Дж);
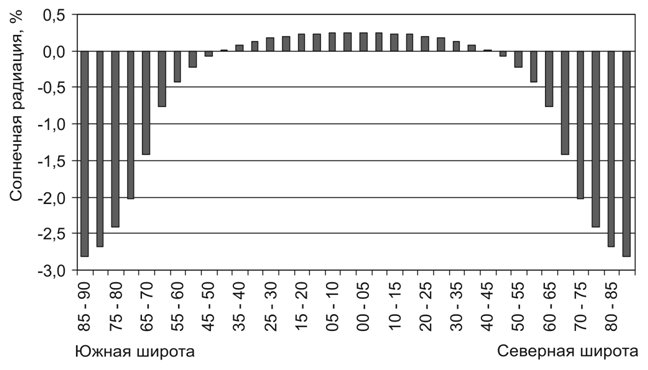
Основные результаты Определено, что за время от 3000 лет до н.э. до 2999 лет н.э. приходящая к Земле за год солнечная радиация сократилась всего на 0,005%. В тоже время распределение приходящей за год радиации по широтным зонам (рис. 1) изменяется более значительно (Федоров, 2014, 2015, а). Поступление солнечной радиации в экваториальную область Земли в настоящее время (в диапазоне, по крайней мере, от 3000 лет до н.э. до 2999 лет н.э.) увеличивается, а в полярные области сокращается (рис. 1). То есть происходит увеличение меридионального градиента инсоляции. Следствием этого эффекта является усиление межширотного теплообмена (между теплыми и холодными областями Земли) как в атмосфере, так и в океане, то есть усиление работы «тепловой машины первого рода» (Шулейкин, 1953; Федоров, 2014). Эффект усиления межширотного теплообмена в атмосфере подтверждается тенденцией увеличения продолжительности меридиональной южной группы циркуляции (Кононова, 2003, 2009, http://www.atmospheric-circulation.ru).
Рис. 1. Изменение инсоляции
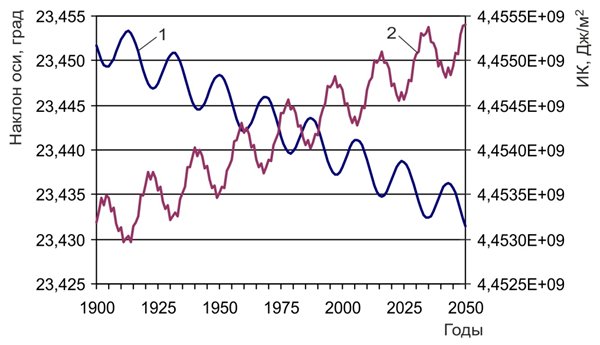
Земли в интервале Отмеченные изменения – усиление широтной контрастности и сглаживание сезонных различий в инсоляции Земли – связаны с вековой тенденцией уменьшения наклона оси вращения Земли в результате прецессии. Известно, что при увеличении угла наклона оси вращения увеличивается приход солнечной радиации в полярные районы, т.е. происходит сглаживание широтной контрастности в полушариях и усиление сезонных различий. При уменьшении угла наклона происходит увеличение радиации, поступающей в экваториальную область, уменьшение радиации поступающей в полярные районы и широтные контрасты возрастают, а сезонные различия сглаживаются (Миланкович, 1939). Для анализа изменения глобальной температуры (приповерхностной температуры воздуха – ПТВ) нами использовалась инсоляционная контрастность (ИК). Для полушарий ИК рассчитывалась как разность солнечной радиации приходящей в область 0° – 45° и приходящей в область 45° – 90° (рис. 2). Для Земли принималось среднее по полушариям значение ИК.
Рис. 2. Изменение угла
наклона оси вращения Земли (1) Изменение инсоляционной контрастности линейно связано с изменением угла наклона оси вращения Земли (коэффициент корреляции R=-0,997). Изменение угла наклона (http://ssd.jpl.nasa.gov) и связанной с ним ИК определяется планетной прецессией (тренд) и нутацией (19-ти летние вариации). Так как динамика ледников во многом определяется температурным режимом, проводился корреляционный анализ значений аномалии ПТВ по данным представленным в архиве университета Восточной Англии и метеобюро Хэдли – массив HadCRUT4 (https://crudata.uea.ac.uk/cru/data/temperature/). Поскольку в исходных рядах ПТВ (и регионально осредненного суммарного баланса массы льда) 19-ти летние вариации не обнаруживаются, проводилось сглаживание рядов угла наклона оси и ИК по 21-му летнему скользящему среднему. Проведенный для достоверных данных (Brohan et al., 2006; Jones et al., 2012) (с 1900 по 2016 гг.) анализ показал наличие высокой корреляционной связи между изменением угла наклона оси и инсоляционной контрастности с изменением аномалии ПТВ (табл. 1). При этом, отмечается отрицательная связь аномалии ПТВ с ИК и положительная связь аномалии ПТВ с углом наклона оси вращения Земли. Аномалия ПТВ в массиве данных представлена относительно средней глобальной температуры для периода 1961 – 1990 гг.
Таблица 1.
Примечание: СП и ЮП – северное и южное полушарие соответственно.
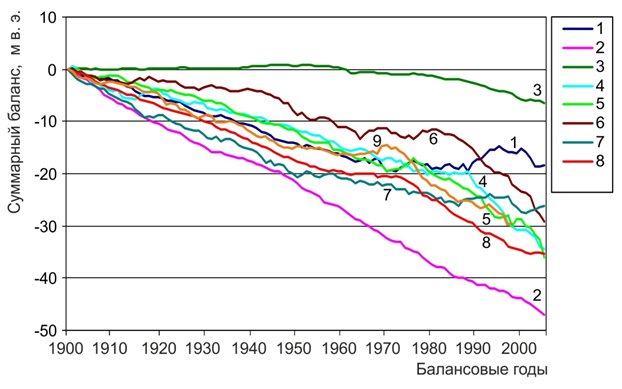
Как показывают наши расчеты, в этих исходных временных рядах аномалии ПТВ (Земли и полушарий) изменчивость в основном (от 69% в Северном полушарии до 85% в Южном полушарии) определяется трендами. На основе балансовых данных (инструментальных наблюдений и реконструкции) для каждого из 9 ледниковых районов северного полушария были получены значения регионально осредненных значений суммарного баланса массы льда (рис 3). Эти значения рассчитывались осреднением годовых значений баланса массы для соответствующих лет по всем охваченным балансовыми наблюдениями ледникам этого района. Всего по 9-ти ледниковым районам для расчетов использовались данные инструментальных балансовых измерений по 125 ледникам приведенные в сборниках «Изменения ледников» (Fluctuations of Glaciers, I – IX, http://wgms.ch/products_fog/, Dyurgerov, 2002) и данные реконструкции по 25 летникам Северного полушария (Федоров, 2011 а, б). Полученные регионально осредненные ряды (с учетом данных реконструкции), охватывают диапазон с 1900 по 2005 гг. (рис. 3). Реконструкция, выполненная на основе по макроциркуляционной модели (Федоров, 2006, 2007, 2009 а, б, 2011 а, б) охватывает период с 1900 года до начала инструментальных балансовых наблюдений в регионе. Полученные данные реконструкции хорошо согласуются с результатами ранее выполненных реконструкций, модельных экспериментов и историческими свидетельствами по динамике ледников (Федоров, 2011 б).
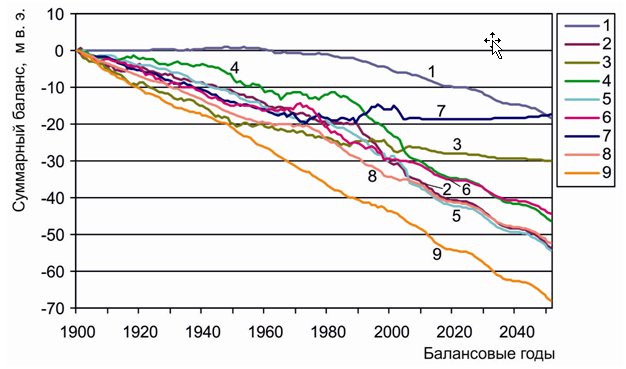
Рис. 3. Динамика регионально
осредненного суммарного баланса массы льда Анализ проводился по временным рядам включающим инструментальные значения суммарного баланса массы и данные реконструкции. Для всех 9-ти ледниковых районов обнаружена тесная связь изменения суммарного баланса массы льда с ИК (табл. 2).
Таблица 2.
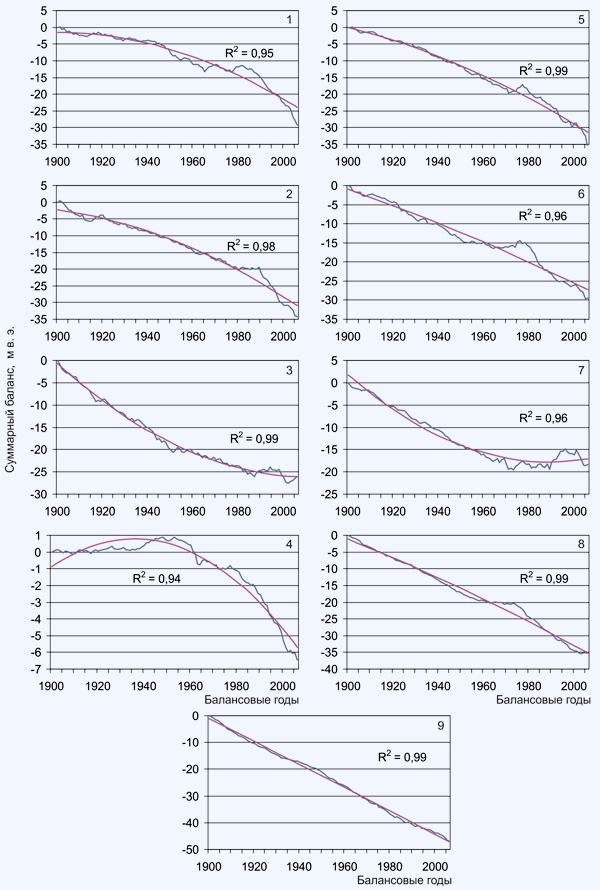
В исходных рядах регионально осредненного суммарного баланса массы изменчивость в основном учитывается трендами линейным и полиномиальным (табл. 2, рис. 4). Приведены значения коэффициента детерминации (R2) показывающего долю изменчивости суммарного баланса массы учитываемую трендом.
Рис. 4. Графики регионально
осредненного суммарного баланса массы льда Таким образом, более 90% изменчивости суммарного баланса массы в исходных для прогноза данных учитывается трендом. В связи с этим корреляционное сопоставление этих трендов с трендами угла наклона оси и ИК (83% – 85% дисперсии в этих рядах также учитывается трендами) представляется оправданным для объяснения причин более чем 90% изменений регионально осредненного суммарного баланса массы льда. На основе найденной корреляционной связи с ИК были построены уравнения регрессии (линейные и полиномиальные – полином 2-й степени) суммарного баланса массы и ИК (табл. 3). Коэффициент детерминации (R2) рассматривают, как правило, в качестве основного показателя, отражающего меру качества регрессионной модели, описывающей связь между зависимой и независимыми переменными модели. R2 показывает, какая доля вариации объясняемой переменной учитывается в модели и, определяется влиянием на нее факторов, включенных в модель (чем ближе R2 к 1, тем выше качество модели). Таблица 3.
Прогноз выполнялся по ансамблю линейных и полиномиальных решений последовательным алгебраическим сложением рассчитанных годовых значений суммарного баланса массы льда (начиная с конечного в исходных рядах значения 2005 года) с суммарным балансом массы исходных рядов (рис. 5). Годовые значения вычислялись по рассчитанным на основе регрессионной модели значениям регионально осредненного суммарного баланса массы льда. В результате получен характер изменения регионально осредненного суммарного баланса массы льда в 9-ти ледниковых районах северного полушария с 1900 по 2050 гг. (рис. 5).
Рис. 5. Таким образом, для среднего (из охваченных балансовыми наблюдениями) по району леднику максимальная потеря льда с 1900 по 2050 гг. отмечается для Шпицбергена 67,9 м в.э. Для регионально осредненного баланса массы льда на Шпицбергене получена линейная зависимость суммарного баланса массы льда от инсоляционной контрастности. Значительные потери льда отмечаются на Аляске (53,6 м в.э.), в Кордильерах (54,2 м в.э.) и на Тянь-Шане (52,4 м в.э.). Несколько меньшие за полтора столетия потери массы льда ожидаются в Альпах (46.3 м в.э.) и на Памиро-Алае (44,5 м.в.э.). На Кавказе потеря льда за этот период составит около 30 м в.э. Минимальные потери льда с начала прошлого столетия до настоящего времени отмечаются в Скандинавии и в Канадском Арктическом архипелаге 17,4 м. в.э. и 18,3 м в.э. соответственно. Скандинавские ледники испытывают сильное влияние Атлантики (Исландского минимума атмосферного давления) определяемого циклоническим переносом с запада и юго-запада морских воздушных масс по Исландско – Карской ложбине (Корякин, 1988; Чижов, 1976). Поэтому здесь потери льда в результате увеличения глобальной ПТВ (абляции) в значительной мере компенсируются увеличением атмосферных осадков (аккумуляцией). Небольшие потери массы льда в Канадском арктическом архипелаге объясняются малыми значениями балансовых показателей. В период с 2017 по 2050 гг. для Скандинавии и Кавказа ожидается стационарное (или близкое к нему) состояние регионально осредненного суммарного баланса массы льда. В Скандинавии потеря массы льда за этот период составит 1,3 м в.э., на Кавказе – около 2,0 м в.э. Минимальные потери льда в этих районах могут определяться усилением циклонической деятельности и переноса морских воздушных масс в районе Скандинавии с Атлантики, на Кавказе со Средиземного моря. Таким образом, связанное с усилением межширотного теплообмена воздействие увеличения ПТВ на ледники (абляции), в этих районах в значительной степени компенсируется увеличением атмосферных осадков (аккумуляцией). Увеличение атмосферных осадков также определяется усилением межширотного теплообмена, в частности, продолжительности действия меридиональной южной группы циркуляции (Кононова, 2009). В других ледниковых районах Северного полушария потери льда за этот период в среднем будут находиться в диапазоне от 9 – 10 м в.э. (Канадский арктический архипелаг, Памиро-Алай) до 12 – 14 м в.э. (Альпы, Аляска, Кордильеры, Шпицберген). Таким образом, в генетическом плане развитие Скандинавских и Кавказских ледников в условиях усиления меридионального переноса тепла и влаги в большей степени связано с атмосферными осадками (аккумуляцией) и в меньшей степени с переносом тепла (абляцией). В остальных ледниковых районах Северного полушария тенденции изменения суммарного баланса массы, в основном определяются переносом тепла (абляцией), связанным с усилением межширотного теплообмена из-за уменьшения наклона оси вращения Земли.
Выводы Отмечена высокая корреляция суммарного баланса массы льда рассчитанного для среднего по ледниковому району леднику (из ледников, охваченных балансовыми наблюдениями), с инсоляционной контрастностью (отрицательная) и изменением угла наклона оси вращения Земли (положительная). Поскольку изменчивость регионально осредненного суммарного баланса массы льда в среднем на 90 – 95% учитывается трендом, то полученные высокие корреляционные показатели указывают на причинно-следственные связи в тенденциях изменения суммарного баланса массы льда и ИК. Таким образом, тенденции изменения суммарного баланса массы льда в ледниковых районах Северного полушария является следствием увеличения инсоляционной контрастности, причиной которого является уменьшение наклона оси вращения Земли. Увеличение инсоляционной контрастности свидетельствует об усилении работы «тепловой машины первого рода» (Шулейкин, 1953) и усилении переноса тепла и влаги (вихревые и циркуляционные потоки в атмосфере, океанические течения) из низких широт в высокие. Следствием этого является повышение температуры в областях стока тепла, увеличение испарения и содержания водяного пара в атмосфере, что приводит к усилению парникового эффекта и дополнительному увеличению температуры в области стока тепла. Следствием этого является деградация современного оледенения в Северном полушарии. В отдельных ледниковых районах (Скандинавия, Кавказ) влияние на динамику массы льда усиления переноса тепла (абляции), отчасти компенсируется усилением переноса влаги – атмосферных осадков (аккумуляции), что приводит к замедлению деградации оледенения. Таким образом, тенденции в деградации современного оледенения в Северном полушарии определяются естественными причинами, основной из которых является уменьшение наклона оси вращения Земли. Полученные результаты важны для обобщенной оценки изменения ледовых ресурсов в будущем, вклада в изменение уровня Мирового океана и для мониторинга климатических изменений в Северном полушарии. Работа выполнена в соответствии с госбюджетной темой «Геоэкологический анализ и прогноз динамики криолитозоны Российской Арктики» (№ АААА-А16-116032810055-0).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
SOLAR RADIATION AND CLIMATE SOLAR THEORY OF CLIMATE CHANGE © www.solar-climate.com |
|
|
|
|
||||||
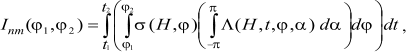 (1)
(1)