| |
СОЛНЕЧНАЯ РАДИАЦИЯ И КЛИМАТ ЗЕМЛИ СОЛЯРНАЯ ТЕОРИЯ ИЗМЕНЕНИЙ
КЛИМАТА |
|
СИНОДИЧЕСКАЯ ВАРИАЦИЯ В МЕЖГОДОВОЙ ИЗМЕНЧИВОСТИ СОЛНЕЧНОЙ ПОСТОЯННОЙ Выполнены теоретические расчеты межгодовой изменчивости солнечной постоянной для 365 точек тропического года в интервале с 1900 по 2050 гг. В результате расчетов в межгодовой изменчивости солнечной постоянной определена вариация, связанная с синодическим лунным периодом. Рассчитаны ее амплитудно – периодические характеристики. Определена фрактальная структура связи межгодовой изменчивости солнечной постоянной и межгодовой изменчивости фазы синодического лунного периода и фрактальная структура межгодовой изменчивости солнечной постоянной.
1. Введение Космо – земному взаимодействию и его проявлению в биосфере Земли посвящено много работ. Например, работы, отражающие проявление в биосфере известного 11-ти летнего цикла солнечной постоянной связанного с изменением активности Солнца (Чижевский, 1976, 1995). Известны, работы, посвященные проявлению в биосфере приливного ритма, связанного с синодическим лунным месяцем (максимальные приливы отмечаются в сизигиях, минимальные в квадратурах) (Марчук, Каган, 1991; Currie, 1988; Brown, 1983). В связи с этим в геофизических и биологических процессах выделяется ритмичность с периодом около 14 суток. Отмечается адаптация биологических видов к этому ритму, наиболее отчетливо проявляющаяся в литорали и прибрежной зоне суши (Нейман, 1984; Neumann, 1981; Агаджанян, Горшков, 1984; Дубров, 1990). Тем не менее, вариации солнечной постоянной определяются двумя причинами, имеющими различную физическую природу. Одна связана с изменением солнечной активности, другая определяется небесно – механическими процессами. В данной работе приводятся результаты, отражающие радиационное содержание, проявляющегося в биосфере ритма, связанного с синодическим лунным месяцем, что дополняет известные представления о его приливном влиянии на биосферу. Солнечная постоянная является мерой солярного климата Земли - приходящей солнечной радиации и ее распределения на верхней границе атмосферы. Приходящая на верхнюю границу атмосферы солнечная радиация характеризует начальные условия для расчетов радиационного баланса Земли и ее геосфер. Солнечная радиация является важнейшим фактором климата, в связи с этим тенденциями и вариациями приходящей, на верхнюю границу атмосферы солнечной радиации могут определяться изменения в глобальном климате Земли. Таким образом, расчет приходящей на верхнюю границу атмосферы представляется важным в проблеме исследования солярного климата Земли и объяснения причин и тенденций изменения глобального климата. С изменением климата меняются и условия обитания всего живого на Земле. Солнечная постоянная – это суммарный поток солнечного излучения, приходящий за единицу времени через единичную площадку, ориентированную перпендикулярно потоку на расстоянии одной астрономической единицы от Солнца вне пределов земной атмосферы (Миланкович, 1939; Кондратьев, 1965; Дроздов и др., 1989; Макарова и др., 1991; Монин, Шишков, 2000). По данным внеатмосферных измерений солнечная постоянная составляет 1367 Вт/м2 (Макарова и др., 1991; Crommelynck, Dewitte, 1997). Солнечная постоянная не является неизменной во времени величиной. Ее вариации определяются двумя основными причинами, имеющими различную физическую природу. Традиционно вариации солнечной постоянной связываются с изменением солнечной активности, то есть с происходящими на Солнце физическими процессами (Willson, 1982; Макарова и др., 1991; Willson, Mordvinov, 2003). Период прямых измерений солнечной постоянной невелик (с 1978 г.). Амплитуда изменения солнечной постоянной на протяжении известного 11-летнего цикла солнечной активности (цикла Швабе – Вольфа), за период измерений в среднем составляет около 1 Вт/м2 или приблизительно 0,07% от величины солнечной постоянной (http://www.pmodwrc.ch). Известны многочисленные публикации посвященные исследованиям связи этой вариации с климатическими изменениями, однако этот вопрос остается дискуссионным (Beer et al., 2000; Foukal et al., 2006; Абдусаматов, 2007; Mackey, 2009: Copp, Lean, 2011). Однако, вариации солнечной постоянной связаны не только с изменением активности Солнца, но и с небесно-механическими процессами, изменяющими расстояние между Солнцем и Землей. При невозмущенном (кеплеровском) движении Земли солнечная постоянная меняется в пределах годового орбитального движения Земли вокруг Солнца с правильным годовым ходом (максимум в перигелии, минимум – в афелии). Реальное орбитальное движение Земли подвержено периодическим возмущениям со стороны Луны и планет, т.е. является возмущенным (Гребенников, Рябов, 1978; Дубошин, 1975; Маров, 1981). В связи с этим Земля год от года в одно и тоже календарное время оказывается на различном расстоянии от Солнца, что является еще одной, до настоящего времени детально не изученной, причиной вариаций солнечной постоянной. Исследования по расчету солнечной постоянной с учетом возмущенного орбитального движения Земли были начаты в Главной геофизической обсерватории имени А.И. Воейкова, однако дальнейшего развития они не получили (Borisenkov et al., 1983, 1985). В настоящее время такие исследования ведутся в МГУ имени М.В. Ломоносова (Федоров, 2012, 2013, 2015 а, б; Fedorov, 2012, 2013, 2014, 2015).
2. Методика расчета Расчеты, поступающей на верхнюю границу
атмосферы радиации, выполнены в упрощенном виде: из предположения, что
Земля является плоским круглым диском (с радиусом равным среднему радиусу
Земли), перпендикуляром к которому является линия, соединяющая центры
Земли и Солнца. По данным астрономических эфемерид – JPL Planetary and
Lunar Ephemerides (DE–406) определялась продолжительность тропических
лет в интервале с 1900 по 2050 гг. (Федоров, 2013).
Тропическим годом является промежуток времени между двумя последовательными
прохождениями центра истинного Солнца через точку весеннего равноденствия
(Бакулин и др., 1983). Каждый тропический год делился на 365 равных
(в каждом году) интервалов (приблизительно соответствующих календарным
суткам). Для начала каждого интервала определялось расстояние от Земли
до Солнца. Точность эфемерид по расстоянию составляет 10-9
а.е. или 0,1496 км (http://ssd.jpl.nasa.gov;
Giorgini et al., 1996). Величина солнечной
постоянной при расстоянии между Землей и Солнцем равном 1 а.е. составляет
По формуле (1) были рассчитаны значения солнечной постоянной на моменты положения Земли в 365 точках каждого тропического года в диапазоне с 1900 по 2050 гг. Последовательным вычитанием значений солнечной постоянной для соответствующих точек были получены ряды значений межгодовой изменчивости солнечной постоянной для 365 точек земной орбиты. Вариации, связанные с изменением солнечной активности не учитывались.
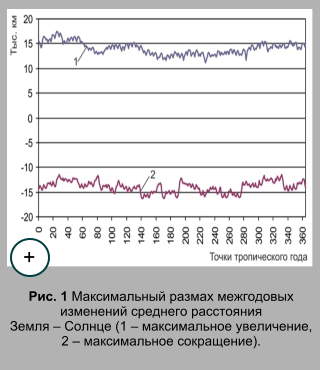
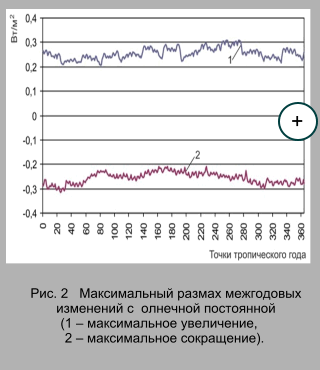
3. Результаты расчетов Из рассчитанных значений расстояния между Землей и Солнцем следует, что в среднем максимальное увеличение расстояния составляет 14,021 тыс. км, а среднее максимальное сокращение – 13,945 тыс. км. Экстремальные значения расстояния Земля – Солнце определялись по 365 точкам для каждого тропического года (с 1900 по 2050 гг.). (рис. 1). Таким образом, в среднем максимальный размах по расстоянию для тропического года составляет около 28 тыс. км. Максимальное увеличение расстояния в массиве (абсолютный максимум) характеризуется величиной 17,370 тыс. км, а сокращение (абсолютный минимум) – 16,255 тыс. км. В соответствии с изменениями расстояния между Землей и Солнцем изменяются значения солнечной постоянной (1). Среднегодовое максимальное увеличение солнечной постоянной составляет 0,255 Вт/м2, среднегодовое максимальное сокращение – 0,256 Вт/м2 (рис. 2).
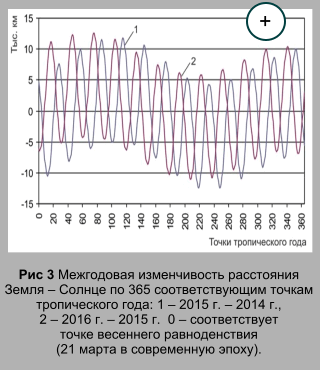
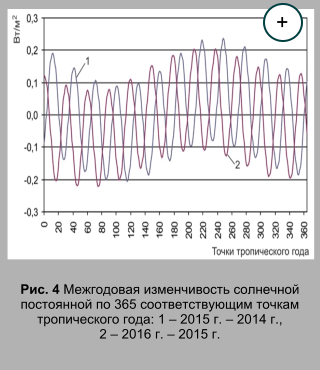
Среднегодовой максимальный размах изменения солнечной постоянной характеризуется величиной 0,511 Вт/м2 (0,037% от величины солнечной постоянной). Максимальное, для исследуемого диапазона (1900 – 2050 гг.), увеличение солнечной постоянной (абсолютный максимум) определяется величиной 0,309 Вт/м2, максимальное сокращение (абсолютный минимум) – 0,315. Максимальный размах межгодовой изменчивости солнечной постоянной составляет 0,624 Вт/м2 (0,046%). Средняя амплитуда межгодовой изменчивости для точки тропического года составляет 8,454 тыс. км (рис. 3). Этому изменению соответствует средняя для точки амплитуда межгодовой изменчивости солнечной постоянной равная 0,155 Вт/м2 (рис. 4). Размах колебаний по расстоянию составляет 16,908 тыс. км, изменчивость солнечной постоянной в среднем определяется диапазоном в 0,310 Вт/м2. Отметим, что амплитуда межгодовой изменчивости солнечной постоянной в 11-ти летнем цикле солнечной активности характеризуется величиной 0,091 Вт/м2. Рассчитанная, приблизительно с суточным разрешением, межгодовая изменчивость расстояния Земля – Солнце и межгодовая изменчивость солнечной постоянной характеризуется строгой периодичностью (рис. 3, 4).
Продолжительность интервалов между максимумами (или между минимумами) характеризуются значениями 29 и 30 суток (интервалов 1/365 продолжительности тропического года). Средняя величина составляет 29,54, что соответствует синодическому лунному месяцу – промежутку времени между двумя последовательными одноименными фазами Луны (Бакулин и др., 1983; Идельсон, 1975). Сравнение положения экстремумов в межгодовой изменчивости солнечной постоянной с разностью геоцентрических долгот Солнца и Луны показывает, что экстремумы связаны с сизигиями (разность долгот 0° – новолуния и 180° – полнолуния). При этом, если межгодовая изменчивость солнечной постоянной определяется вычитанием значений предыдущего года из соответствующих значений последующего, максимумы межгодовой изменчивости всегда располагаются между новолуниями предыдущего года и ближайшими полнолуниями последующего (эти фазы год от года смещаются на 3 – 5 суток по ходу года). Минимумы межгодовой изменчивости всегда располагаются между полнолуниями предшествующего года и новолуниями последующего (табл. 1).
Табл. 1 Межгодовая изменчивость солнечной постоянной и фазы синодического лунного месяца (фрагмент).
Примечание: цветом выделены экстремумы межгодовой изменчивости солнечной постоянной.
Таким образом, экстремумы межгодовой изменчивости солнечной постоянной во всех случаях либо опережают сизигию последующего года, либо совпадают с ней (но никогда по отношению к ней не запаздывают). При этом совпадение экстремумов с новолунием или полнолунием последующего года отмечается в 4,79% случаев. Опережение экстремумов на сутки новолуний и полнолуний последующего года отмечается в 63,90% случаев, на двое суток – в 31,31% случаев. При вычитании значений последующего года из соответствующих значений предыдущего года наблюдается обратная картина: максимумы отмечаются между полнолуниями предшествующего года и ближайшими новолуниями последующего, минимумы между полнолуниями предшествующего года и полнолуниями последующего. Отмечается чередование экстремумов, в межгодовой изменчивости солнечной постоянной от года к году, со смещением по ходу года на 3 – 5 суток и сменой знака экстремума (рис. 3, 4). Если, например, в определенной точке года отмечается максимум межгодовой изменчивости, то в следующем году, со смещением от этой точки на 3 – 5 суток по ходу года в межгодовой изменчивости, будет отмечаться минимум и т. д. При этом, смещение в 3 суток отмечается в 23,1%, в 4 суток в 69,8%, в 5 суток – в 7,1% случаев (в среднем 3,8 сут). Отмеченная связь экстремумов межгодовой изменчивости солнечной постоянной с сизигиями объясняется следующим образом. Известно, что Земля и Луна с годовым периодом вращаются вокруг центра масс Земля, Луна и Солнце. Это движение происходит под действием двух сил: силы притяжения и центробежной силы. Во время новолуния Луна оказывается ближе к Солнцу (центру вращения). Для сохранения момента импульса в системе Земля – Луна, необходимо увеличение расстояния между Землей и Солнцем (центром вращения). Солнечная постоянная при этом уменьшается. Во время полнолуния Земля оказывается ближе к Солнцу (сильнее притягивается, чем в новолуние и, вследствие этого смещается в сторону Солнца относительно среднего радиуса вращения), поэтому солнечная постоянная увеличивается. В связи с этим если в текущем году в определенных точках тропического года (орбиты) отмечается новолуние, а в предыдущем, следовательно, вблизи этих точек (3 – 5 суток) отмечалось полнолуние, то в межгодовой изменчивости (при вычитании предыдущего года из текущего) отмечается максимум. В обратном случае – минимум.
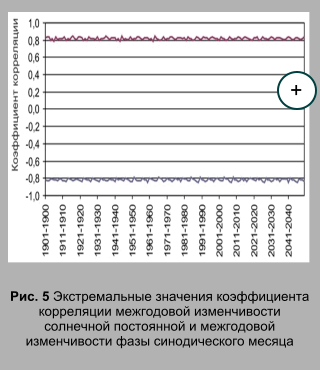
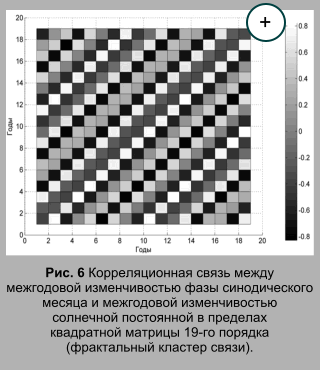
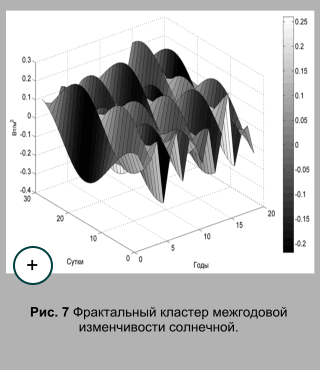
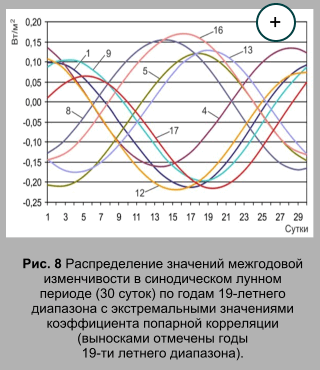
Для определения связи межгодовой изменчивости фазы синодического лунного месяца (периода) и межгодовой изменчивости солнечной постоянной рассчитывалась попарная корреляция их показателей за период с 1900 по 2050 гг. В результате была сформирована матрица, включающая 150 строк и 150 столбцов значений коэффициента корреляции, по которой определялись экстремальные значения коэффициента корреляции (рис. 5). Значения коэффициента корреляции в матрице изменяются в диапазоне ограниченном экстремальными значениями (рис. 5). При анализе рассчитанной матрицы обнаруживается, что весь массив значений коэффициента корреляции состоит из обладающих подобием фрагментов, которые представляют собой квадратные матрицы 19-го порядка (фрактальная матрица связи). Эти фрагменты или фрактальные кластеры (Смирнов, 1986) включают значения коэффициента попарной корреляции для каждого из 19-ти рядов межгодовой изменчивости солнечной постоянной с каждым из 19-ти рядов межгодовой изменчивости фазы синодического месяца (рис. 6). Такая структура фрактального множества называется пертайлингом по терминологии Б. Мандельброта (Мандельброт, 2002). Таким образом, связь между межгодовой изменчивостью солнечной постоянной и межгодовой изменчивостью фазы синодического месяца найдена в форме матрицы, обладающей сложной, но закономерной – фрактальной структурой. В физике широко известны представления о фрактальной структуре в природе, то есть, о кластеризации и самоподобии в пространстве, масштабно-инвариантных объектах (Фракталы в физике, 1988; Федер, 1991; Божокин, Паршин, 2001; Мандельброд, 2002). Представления о фрактальной структуре процессов создают основы, позволяющие проводить более глубокий анализ исследуемых систем и явлений (Зельдович, Соколов. 1985;Смирнов, 1986; Олемский, Флат, 1993; Зосимов, Лямшев, 1995). В данной статье рассматриваются примеры фрактальной хронологии в природе, то есть кластеризации и подобия во времени, хронологически-инвариантных объектах. Поэтому понятие фрактальной размерности, имеющее отношение к пространству не рассматривается. Фрактальная структура массива данных, вероятно, определяется (генерируется) нутационным циклом, отражающим изменения расстояния между Землей и Солнцем и, соответствующие им изменения солнечной постоянной (Федоров, 2015). Тем не менее, выделенный фрагмент, представляющий фрактальный кластер связи межгодовой изменчивости солнечной постоянной и межгодовой изменчивости фазы синодического лунного периода, обладает возможностями дальнейшей детализации (фрагментации). Анализ массива значений межгодовой изменчивости солнечной постоянной для 365 точек тропического года в диапазоне с 1900 по 2050 гг. показывает, что этот массив также состоит из чередования самоподобных во времени фрагментов (фрактальных кластеров). Таким образом, матричный массив межгодовой изменчивости солнечной постоянной имеет фрактальную структуру. Основные фрактальные кластеры представляют собой прямоугольную матрицу значений межгодовой изменчивости солнечной постоянной для 29 или 30 точек тропического года (соответствует синодическому лунному периоду или месяцу) в 19-летнем диапазоне. На рис. 7 фрактальный кластер межгодовой изменчивости солнечной постоянной представлен в виде поверхности. Корреляционный анализ структуры межгодовой изменчивости солнечной постоянной проводился на примере фрактального кластера с размерами по продолжительности (по времени) в 30 точек (суток) и 19 лет. Для этого фрагмента рассчитывались значения коэффициента попарной корреляции для рядов значений межгодовой изменчивости, представленных в столбцах фрактальной матрицы (т. е., по годам). Результаты показывают, что первый год фрактального кластера характеризуется высокими положительными связями с четвертым (0,817), девятым (0,950), двенадцатым (0,967) и семнадцатым (0,828) годами фрагмента (рис. 8).
Высокие отрицательные значения коэффициента попарной корреляции определяются для первого года с пятым (-0,962), восьмым (-0,848), тринадцатым (-0,872) и шестнадцатым (-0,931) годами фрактала. Для второго года фрактальной матрицы, отмеченные высокие значения корреляции отмечаются уже для пятого, десятого, тринадцатого и восемнадцатого голов, отрицательные для шестого, девятого, четырнадцатого и семнадцатого годов. Подобная структура связи характерна для всего массива межгодовой изменчивости солнечной постоянной с суточным разрешением. Всего в 19-ти летнем диапазоне выделяется 8 отдельных лет, в которых значения межгодовой изменчивости солнечной постоянной в синодическом месяце имеют высокую положительную или отрицательную корреляционную связь с первым годом фрактала. То есть выделяются годы с подобным распределением значений межгодовой изменчивости солнечной постоянной в пределах синодического месяца (с некоторым смещением по фазе) и, годы с обратным подобному, распределением. Анализ связи межгодовой изменчивости солнечной постоянной по строкам массивы (т. е., по суткам) также выявляет определенные закономерности в распределении хронологического подобия. Так в первые, вторые, третьи, четвертые, двадцать восьмые, двадцать девятые и тридцатые сутки синодического периода отмечается в общем сходное (подобное) распределение межгодовой изменчивости солнечной постоянной в 19-ти летнем диапазоне (рис. 9).
Проводилась оценка подобия выделенных фрактальных кластеров, которая сводилась к следующим действиям. Рассчитывались средние по модулю фрактальные кластеры. Во множестве фрактальной связи межгодовой изменчивости солнечной постоянной и межгодовой изменчивости фазы синодического лунного периода среднее определялось по 49 кластерам множества (квадратным матрицам 19 порядка, 361 ячейка), во множестве межгодовой изменчивости солнечной постоянной по 84 кластерам (размер кластера 19 лет и 30 суток, 570 ячеек). Затем рассчитывались модули разности между каждым фрактальным кластером и средним фрактальным кластером, и находилась средняя по модулю матрица разности. Далее рассчитывалась среднее по модулю значений для ячейки в средней матрице разности и в среднем фрактальном кластере. Оценка подобия рассчитывалась делением среднего по модулю значению ячейки средней матрицы разности на среднее по модулю значение ячейки среднего фрактального кластера. Умножением на 100 оценка подобия выражалась в процентах. Для фрактального множества связи межгодовой изменчивости солнечной постоянной и межгодовой изменчивость фазы синодического лунного периода, полученная оценка составила 6,48%, для фрактального множества межгодовой изменчивости солнечной постоянной – 44,07%. Таким образом, по принятому критерию оценки подобия фрактальные кластеры в первом множестве подобны на 93,52%, во втором на 55,93%. Известно, что амплитуда 11-ти летнего цикла солнечной постоянной характеризуется значением близким к 1 Вт/м2 (Макарова и др., 1991; http://www.pmodwrc.ch). Следовательно межгодовая изменчивость в 11-летнем цикле солнечной активности характеризуется средней величиной размаха равной 0,182 Вт/м2 (0,013% солнечной постоянной). Это значение в 3,42 раза уступает абсолютному максимальному размаху (0,624 Вт/м2), в 2,81 раза уступает среднему максимальному размаху (0,511 Вт/м2) и в 1,70 раза или на 0,010% от величины солнечной постоянной меньше среднего размаха синодической вариации (0,310 Вт/м2 или 0,023%). Таким образом, синодическая вариация представляется значимой в межгодовой изменчивости солнечной постоянной.
4. Заключение В результате расчетов в межгодовой изменчивости солнечной постоянной определена вариация, связанная с синодическим лунным периодом. Рассчитаны ее амплитудно – периодические характеристики. Определена фрактальная структура связи межгодовой изменчивости солнечной постоянной и межгодовой изменчивости фазы синодического лунного периода. Показана фрактальная структура межгодовой изменчивости солнечной постоянной. В пределах фрактальных кластеров межгодовой изменчивости солнечной постоянной найдены годы 19-ти летнего диапазона (нутационного цикла), для синодических периодов которых отмечаются высокие положительные или отрицательные корреляционные связи. Выделены сутки синодического лунного периода, в которых отмечается сходная (подобная) межгодовая изменчивость для всех лет 19-ти летнего диапазона. Таким образом, определены свойства исследуемых фрактальных кластеров. Причина фрактальной структуры солнечной постоянной во времени (фрактальной хронологии) связана с естественными природными ритмами, определяемыми небесно-механическими процессами (генераторами). Следствием синодической вариации солнечной постоянной может быть изменение начальных радиационных условий в одних и тех же точках тропического года влияющих на развитие климатических, синоптических и биологических процессов. Автор выражает благодарность И.К. Бариеву и Д.М. Фролову за помощь в подготовке графических иллюстраций.
|
|
SOLAR RADIATION AND CLIMATE SOLAR THEORY OF CLIMATE CHANGE © www.solar-climate.com |
|
|
|
|
||||||
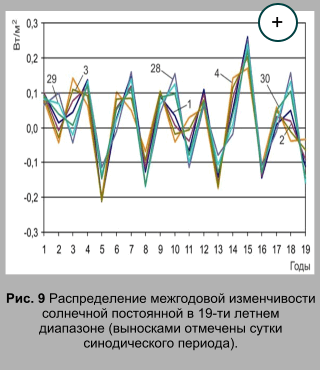 Распределение значений межгодовой изменчивости солнечной постоянной
в первые сутки синодического периода (по годам 19-ти летнего диапазона)
характеризуется высокими положительными корреляционными связями с распределением
во вторые (0.982), третьи (0,921), четвертые (0,810), двадцать восьмые
(0.862), двадцать девятые (0,924) и тридцатые (0,955). Подобная связь
отмечается также для первых суток с двадцать восьмыми, двадцать девятыми
и тридцатыми сутками предыдущего фрактала. В пределах еще одних – двух
суток (пятые, двадцать шестые и двадцать седьмые) связь распределения
характеризуется значениями коэффициента корреляции около 0,6. Для пятых,
например, суток синодического месяца подобие уже отмечается со вторыми
(0,779), третьими (0,891), четвертыми (0,971), шестыми (0,970), седьмыми
(0,888) и восьмыми (0,768) сутками и т. д. То есть, связь распределение
межгодовой изменчивости солнечной постоянной в 19-ти летнем диапазоне
характеризуется подобием приблизительно для 7 соседних суток синодического
месяца.
Распределение значений межгодовой изменчивости солнечной постоянной
в первые сутки синодического периода (по годам 19-ти летнего диапазона)
характеризуется высокими положительными корреляционными связями с распределением
во вторые (0.982), третьи (0,921), четвертые (0,810), двадцать восьмые
(0.862), двадцать девятые (0,924) и тридцатые (0,955). Подобная связь
отмечается также для первых суток с двадцать восьмыми, двадцать девятыми
и тридцатыми сутками предыдущего фрактала. В пределах еще одних – двух
суток (пятые, двадцать шестые и двадцать седьмые) связь распределения
характеризуется значениями коэффициента корреляции около 0,6. Для пятых,
например, суток синодического месяца подобие уже отмечается со вторыми
(0,779), третьими (0,891), четвертыми (0,971), шестыми (0,970), седьмыми
(0,888) и восьмыми (0,768) сутками и т. д. То есть, связь распределение
межгодовой изменчивости солнечной постоянной в 19-ти летнем диапазоне
характеризуется подобием приблизительно для 7 соседних суток синодического
месяца.





