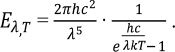Лучистая энергия

Свечение тел при их нагревании называется температурным или тепловым излучением. В этом случае энергия внутренних хаотических тепловых движений частиц тела (при ) непрерывно переходит в энергию испускаемого электромагнитного излучения. Основной количественной характеристикой теплового излучения тела является его лучеиспускательная способность , т.е. лучистая энергия, испускаемая единицей поверхности тела за единицу времени (эрг/см² ∙ сек или Дж/м² ∙ сек = Вт/м²) при температуре тела . Эта энергия переносится электромагнитными волнами различной длины и при изучении излучения полная лучеиспускательная способность тела анализируется в различных диапазонах длин волн. Энергия электромагнитных волн с длиной от до , испускаемая единицей поверхности излучающего тела за единицу времени, пропорциональна величине выделенного интервала длин волн:

Коэффициент пропорциональности есть лучеиспускательная способность тела при данной температуре для данной длины волны , и имеет размерность Вт/м³. Полная лучеиспускательная способность тела складывается из элементарных интервалов , т.е.

где интеграл распространен на весь бесконечный интервал всевозможных длин волн (Зисман, Тодес, 1970; Ландсберг, 1973, 2000; Сивухин, 2002).

С ростом температуры увеличивается интенсивность теплового движения частиц и, возрастает энергия, излучаемая телом во всем диапазоне излучаемых электромагнитных волн. При абсолютном нуле температуры тепловое излучение отсутствует и .

При тепловом излучении энергия теплового движения в теле переходит в энергию испускаемых электромагнитных волн. При поглощении света происходит обратный процесс перехода лучистой энергии в тепловую энергию тела. В обоих случаях взаимные превращения тепловой и лучистой энергии протекают через промежуточную стадию колебания электрических зарядов в теле. Поэтому лучеиспускательная и лучепоглощательная способности тела обусловлены одними и теми же деталями его строения и тесно связаны между собой. При этом отношение полной лучеиспускательной способности любого тела к его же поглощательной способности при данной температуре есть величина постоянная, равная испускательной способности абсолютно черного тела при той же самой температуре. Это соотношение было найдено в 1860 году Г. Кирхгофом (Kirchhof). Закон, названный его именем, формулируется следующим образом. Отношение лучеиспускательной и поглощательной способности для любых тел при одинаковой их температуре и для одной и той же длины волны одинаково и не зависит от природы этих тел. Это отношение является универсальной функцией длины волны и температуры и равно лучеиспускательной способности абсолютно черного тела  

Поскольку для абсолютно черного тела лучепоглощение (поглощает все падающие на него лучи), а для других тел , то из закона Кирхгофа следует весьма важное утверждение. Излучение, которое тело сильнее поглощает, сильнее и испускается. При данной температуре 

т.е. тепловое излучение абсолютно черного тела во всех частях спектра интенсивнее, чем для нечерного тела, нагретого до той же самой температуры.

В 1878 году Й. Стефаном (Stefan), а в 1884 году Л. Больцманом (Boltzmann) была доказана пропорциональность полной лучеиспускательной способности абсолютно черного тела четвертой степени его абсолютной температуры т.е.

Это соотношение получило название закона Стефана – Больцмана.

Исследуя спектральное распределение излучения В. Вин (Wien) показал, что максимум лучеиспускательной способности находится на некоторой длине волны , которая связано с абсолютной температурой соотношением

Таким образом, с ростом температуры максимум лучеиспускательной способности абсолютно черного тела смещается в сторону более коротких волн. Это соотношение получило название закона смещения Вина (Кондратьев, Филипович, 1960; Зисман, Тодес, 1970; Ландсберг, 1973, 2000; Сивухин, 2002).

Это законы волновой электромагнитной теории света. Однако, физики столкнулись с проблемами при изучении излучения с короткими длинами волн («ультрафиолетовая катастрофа»), что указало на теоретические дефекты и необходимость пересмотра принципиальных положений этой теории. В 1901 году М. Планк высказал предположение о том, что излучение испускается телами не непрерывно, но в виде отдельных порций (дискретно). Энергия каждой такой порции – кванта излучения – пропорциональна его частоте:

, где   - универсальная постоянная, одинаковая по всему спектру и получившая впоследствии название постоянной Планка (6,62 ∙ 10^-34 Дж ∙ сек). В результате Планк получил выражение для лучеиспускательной способности абсолютно черного тела (формула Планка):

Согласно формуле Планка для каждой данной длины волны λ с ростом температуры показатель  и величина, стоящая в знаменателе, , убывают, а сама дробь возрастает. Следовательно, с ростом температуры возрастает и лучеиспускательная способность во всех участках спектра, но в различной степени. Из формулы Планка вытекают также законы теплового излучения Стефана – Больцмана и Вина (Кондратьев, Филипович, 1960; Кондратьев, 1954, 1965; Бакулин и др., 1966, 1983; Хргиан, 1986; Зисман, Тодес, 1970; Ландсберг, 2000; Сивухин, 2002).

Распространение излучения

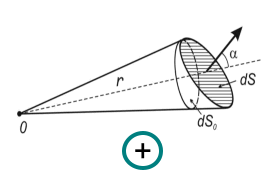
Для пространственных задач распространения излучения существенно понятие о телесном угле (Перрен де Бришамбо, 1966; Зисман, Тодес, 1970; Ландсберг, 1973). Мерой телесного угла является отношение площади участка, вырезаемого конусом на поверхности сферы к квадрату ее радиуса , т.е.  (рис. 1). За единицу телесного угла принят телесный угол, опирающийся на участок поверхности сферы, площадь которого равна квадрату ее радиуса ()Эта единица называется стерадиан (стер). Наибольший телесный угол равен, очевидно, стер (площадь всей поверхности сферы ).

Как видно из рисунка 1 площадка , нормаль к которой   составляет угол  с радиусом , проведенным из точки наблюдения 0 , видна из этой точки 0, под телесным углом 

. (1)

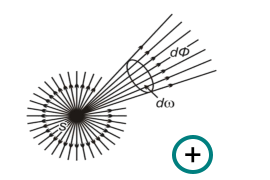
Основной энергетической величиной излучения является лучистый поток   (Миланкович, 1939; Кондратьев, 1965; Зисман, Тодес, 1970; Ландсберг, 2000) Эта величина характеризует энергию, проходящую через данную поверхность за единицу времени, и измеряется соответственно в единицах мощности (Вт, эрг/сек).

На рис. 2 изображен точечный источник и, выделен телесный угол с вершиной в точке .

Если обозначить лучистый поток, заключенный в телесном угле , через , тогда соотношение   является силой излучения точечного источника в данном направлении. Из этого соотношения следует, что сила излучения характеризуется величиной потока, заключенного в единице телесного угла, и измеряется соответственно в Вт/стер или эрг/сек ∙ стер. Если поток, испускаемый точечным источником, равномерный во всех направлениях, то ,  (2)

где  - полный лучистый поток, испускаемый источником по всем направлениям, т.е. во всем телесном угле . Если же поток неравномерен, то формула (2) определяет среднюю силу излучения источника.

Интенсивность излучения протяженного источника характеризуется его лучистостью. Она численно равна силе излучения в данном направлении, создаваемой единицей площади видимой поверхности источника (измеряется в Вт/м² ∙ стер или эрг/сек ∙ см² ∙ стер). Лучистость протяженного источника может быть различной в разных направлениях. Однако, для таких источников, как Солнце величина лучистости не зависит от направления наблюдения. Т.е. сила излучения (света) такого источника пропорциональна косинусу угла с нормалью (закон Ламберта) и максимальна в направлении нормали. Если поверхность испускает лучистый поток по всем направлениям (в телесном угле ), то лучистый поток, испускаемый единицей площади, характеризует плотность излучения (светимость) источника и измеряется в Вт/м² или эрг/см² ∙ сек.

Понятие облученности (освещенности) относится уже не к источникам излучения (света), а характеризует интенсивность лучистой энергии, падающей на освещаемую поверхность. Величина численно равна величине потока, падающего на единицу освещаемой поверхности, т.е.   (измеряется в Вт/м² или эрг/сек ∙ см²).

Если произвольно ориентированная в пространстве площадка   освещается точечным источником 0  (рис 1.), то согласно формуле (1) , где – расстояние от источника до площадки, - угол между направлением лучей и нормалью к площадке, а  - телесный угол, под которым видна площадка  из точечного источника 0 . Освещенность этой поверхности

 (3)

так как есть сила света источника .

Формула (3) выражает два закона освещенности:

1. Освещенность площадки обратно пропорциональна квадрату расстояния от точечного источника (закон обратных квадратов)

2. Освещенность площадки прямо пропорциональна косинусу угла между направлением лучистого потока и нормалью к площадке (закон косинуса).

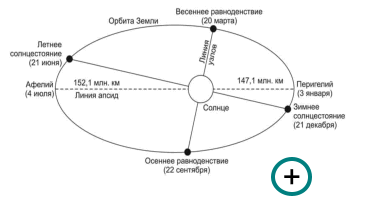
Солярный климат Земли

Под солярным климатом понимается рассчитываемое теоретически поступление и распределение солнечной радиации на верхней границе атмосферы или на поверхности Земли в отсутствии атмосферы. (Алисов, Полтараус, 1974; Хромов, Петросянц, 2006).

Солнце по своим лучеиспускательным свойствам близко к абсолютно черному телу. Распределение энергии в спектре солнечной радиации (до поступления ее в атмосферу) достаточно близко к теоретически полученному для абсолютно черного тела при температуре 6000 ^оК. Максимум лучистой энергии приходится в обоих случаях на диапазоны с длинами волн около 0,47 мк (зелено-голубые лучи видимой части спектра). Однако в ультрафиолетовом диапазоне солнечного спектра энергии существенно меньше, чем в ультрафиолетовой области спектра абсолютно черного тела при температуре 6000 ^оК. Таким образом, Солнце в точности не является абсолютно черным телом. Однако указанную температуру (6000 ^оК) принято считать близкой к реальной температуре на поверхности Солнца (Эйгенсон, 1963; Хромов, 1968; Кондратьев, 1965; Гарвей, 1982; Хргиан, 1986; Хромов, Петросянц, 2006).

В спектральном составе солнечной радиации на интервал длин волн между 0,1 и 4 мк приходится 99% всей энергии солнечной радиации. Всего 1% остается на радиацию с меньшими и большими длинами волн, вплоть до рентгеновских лучей и радиоволн. Видимый свет занимает узкий интервал длин волн, всего от 0,4 до 0,75 мк. Однако в этом интервале заключается почти половина всей солнечной лучистой энергии (46%). Почти столько же (47%) приходится на инфракрасные лучи, а остальные 7% - на ультрафиолетовые (Хромов, 1968; Гарвей, 1982; Хромов, Петросянц, 2006). Видимое излучение Солнца отличается большим постоянством (изменение его светимости составляет не более 2%). Ультрафиолетовая и рентгеновская области спектра более значительно изменяются с изменением активности Солнца. Изменяется также интенсивность корпускулярного излучения. Солнечная активность проявляется в ряде образований, возникающих в атмосфере Солнца: солнечные пятна, факелы, флоккулы, вспышки (Струве и др., 1967; Бакулин и др., 1983; Ермолаев, 1975; Неклюкова, 1976; Поток энергии Солнца.., 1980; Ливингстон, 1982; Макарова и др., 1991; Мордвинов, 1998; Foukal, 2004).

Солярный климат Земли определяется распределением лучистой энергии Солнца, поступающей на внешнюю границу земной атмосферы. Солнце непрерывно излучает в мировое пространство энергию, мощность потока которой приблизительно составляет 3,94 ∙ 10²⁶ Вт. На диск Земли приходится часть этой энергии равная произведению солнечной постоянной на площадь большого круга Земли. При среднем радиусе Земли равном 6371 км, площадь большого круга составляет 1,275 ∙ 10¹⁴ м², а приходящая на нее лучистая энергия равна 1,743 ∙ 10¹⁷ Вт. Годовой приход солнечной радиации на верхнюю границу атмосферы Земли составляет 5,49 ∙ 10²⁴ Дж. (Дроздов и др., 1989; Хромов, Петросянц, 2006; Абдусаматов, 2009).

Мерой солярного климата является солнечная постоянная, представляющая поток (другие названия: плотность потока радиации, интенсивность) солнечной радиации на внешней границе атмосферы (Алисов, Полтараус, 1974). Размеры Земли и Солнца очень малы по сравнению с расстоянием между ними, поэтому можно считать падающие на Землю солнечные лучи параллельными. Солнечная постоянная, таким образом – это полное количество солнечной энергии по всему спектру, падающее за единицу времени на единицу площади перпендикулярную солнечным лучам на среднем расстоянии Земли от Солнца за пределами земной атмосферы. (Миланкович, 1939; Алисов и др., 1952; Кондратьев, 1965; Эдди, 1980; Фрёлих, 1980; Монин, 1982; Бакулин и др., 1983).

Солнечная постоянная зависит от излучательной способности Солнца и от расстояния между Землей и Солнцем. Излучательная способность Солнца (солнечная активность) периодически меняется. Заметили это, прежде всего по изменениям числа солнечных пятен и даже установили средний период изменений равный 11 годам. Это оказалось верным для всего комплекса солнечной активности: распространенность факелов и флоккул, частота вспышек, количество протуберанцев, форма короны. Но так как интервалы между максимумами солнечной активности колеблются от 7 до 17 лет, а между минимумами от 9 до 14, правильнее говорить о ее 11-летнем цикле (цикл Швабе – Вольфа), а не периодичности. Выделяются и другие циклы, но вопрос о периодизации солнечной активности нельзя считать завершенным (Ермолаев, 1975; Неклюкова, 1976; Гриббин, 1980; Витинский, 1983; Полтараус, Кислов, 1986; Хргиан, 1986; Кондратьев, 1987; Макарова и др., 1991; Предстоящие изменения.., 1991; Абдусаматов, 2009).

Если обозначить – среднее расстояние между Землей и Солнцем, то при другом расстоянии поток солнечной радиации составит .Выражение характеризует уменьшение плотности потока излучения при увеличении расстояния от Солнца (Полтараус, Кислов, 1986; Хргиан, 1986).

Земля вращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце (рис. 3). В начале января (в современную эпоху) она наиболее близка к Солнцу (147 млн. км), в начале июля – наиболее далека от него (152 млн.км).

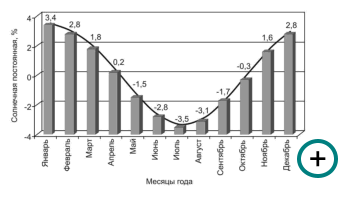
Так как интенсивность радиации меняется обратно пропорционально квадрату расстояния, то солнечная постоянная в течение года меняется и имеет правильный годовой ход (Алисов и др., 1952; Кондратьев, 1965; Кислов, 2001; Хромов, Петросянц, 2006). Отклонение интенсивности солнечной радиации на внешней границе атмосферы от средней величины солнечной постоянной (амплитуда годовой вариации) составляет около 3,5% (рис. 4). В январе солнечная постоянная приблизительно на 0,07 кал/см² ∙ мин (около 49 Вт/м²) больше, а в июле на такую же величину меньше, чем при среднем расстоянии между Землей и Солнцем. Это годовая вариация, связанная с эллиптическим движением и изменением расстояний между Землей и Солнцем в течение года (афелий – перигелий).

По данным внеатмосферных наблюдений солнечная постоянная составляет 1367 Вт/м² ( 0,3%) или 1,959 кал/см² мин (Хромов,1968; Lamb, 1972; Stringer, 1972; Витвицкий, 1980; Полтараус, Кислов, 1986; Кислов, 2001; Хромов, Петросянц, 2006). Это значение используется и в наших исследованиях.

 Солнечная постоянная определяется соотношением:

где - постоянная Стефана – Больцмана, – астрономическая единица, – радиус Солнца, – эффективная температура фотосферы (Абдусаматов, 2009).

В солярном климате выражена асимметрия в инсоляции полугодий. В летнее полугодие (для северного полушария) при орбитальном движении от точки весеннего равноденствия к точке летнего солнцестояния и далее – к точке осеннего равноденствия, Земля проходит окрестности афелия своей орбиты, то есть находиться на большем расстоянии  от Солнца (около 1,52 ∙10¹³см). В зимнее (для северного полушария) полугодие, когда Земля проходит путь от точки осеннего равноденствия к точке зимнего солнцестояния (рис. 3) и далее к точке весеннего равноденствия, она проходит окрестности перигелия орбиты, то есть, находится на наименьшем расстоянии от Солнца (около 1,47 ∙10¹³см). При отмеченном изменении расстояния Земля, в зимнее (для северного полушария) полугодие, должна получать большее количество энергии, чем в летнее, в связи с соответствующими расстояниям изменениями солнечной постоянной. Принято считать, что в связи с тем, что летнее (для северного полушария) полугодие продолжительнее зимнего (186 и 179 суток соответственно), в целом за год эти различия в притоке общей солнечной энергии на верхнюю границу атмосферы между полугодиями сглаживаются. То есть, в течение года полугодия получают одинаковое количество суммарной солнечной радиации (Перен де Бришамбо, 1966; Монин, Шишков, 1979; Монин, 1982; Полтараус, Кислов, 1986). Это следует и из второго закона Кеплера для невозмущенного движения.

Другой характерной особенностью распределения инсоляции является сезонность. Выделяются четыре астрономических сезона (весенний, летний, осенний и зимний), разделяемых положением Солнца на эклиптике в кардинальных точках ( - точка весеннего равноденствия; - точка летнего солнцестояния; - точка осеннего равноденствия; - точка зимнего солнцестояния; - долгота Солнца на эклиптике, отсчитываемая от точки весеннего равноденствия в сторону, противоположную суточному движению небесной сферы). При этом, из второго закона (закона площадей) Кеплера для невозмущенного движения следует, что инсоляция весной в точности равна инсоляции в течение лета, а инсоляция осенью – зимней инсоляции (Перен де Бришамбо, 1966; Монин, Шишков, 1979; Монин, 1982; Полтараус, Кислов, 1986).

Изменение расстояния между Землей и Солнцем связанное с многовековыми колебаниями элементов земной орбиты: наклона экватора к эклиптике, эксцентриситета и долгота перигелия приводит к соответствующим изменениям в поступлении  солнечной радиации к Земле (астрономическая теория климата). Суммарная годовая инсоляция при этом остается неизменной, происходит лишь ее перераспределение между сезонами и различными широтными зонами Земли (Полтараус, Кислов. 1986). Это действительно справедливо, но только если рассматривать такие многовековые колебания по отношению к кеплеровскому, невозмущенному движению Земли.

Таким образом, в современной геофизике и климатологии солярный климат рассматривается, в основном, исходя из представлений о невозмущенном (кеплеровском) движении Земли по эллиптической орбите. Однако, реальное движение Земли является, по крайней мере, возмущенным. В этом случае, отмеченные для невозмущенного движения соотношения в поступлениях солнечной энергии за сезоны, полугодия (энергетическое равенство) и годы, строго не выполняются. Поэтому одной из основных задач исследования солярного климата Земли (исходя из его определения) является выполнение расчетов солнечной радиации приходящей на верхнюю границу атмосферы Земли с учетом ее возмущенного движения на интервале времени малой продолжительности. Эти расчеты позволяют определить реальные энергетические соотношения между астрономическими сезонами, полугодиями и тропическими годами в отдельных широтных зонах, полушариях и на Земле в целом. Для изучения динамики солярного климата с учетом возмущенного орбитального движения Земли и поисков связи изменений глобального климата Земли с вариациями ее солярного климата подобные расчеты представляются вполне актуальными (Кондратьев, 1987)

Литература.

Абдусаматов Х.И. Солнце диктует климат Земли. – СПб.: – Логос, 2009. – 197 с.

Алисов Б.П., Дроздов О.А., Рубинштейн Е.С. Курс климатологии. – Л.: Гидрометеоиздат, 1952. – 488 с.

Алисов Б.П, Полтараус Б.В. Климатология. – М.: Московский университет, 1974. – 210 с.

Бакулин П.И., Кононович Э.В., Мороз В.И. Курс общей астрономии. – М.: Наука, 1966. – 528 с.

Бакулин П.И., Кононович Э.В., Мороз В.И. Курс общей астрономии. – М.: Наука, 1983. – 560 с.

Витвицкий Г.Н. Зональность климата Земли. – М.: Мысль, 1980. – 253 с.

Витинский Ю.И. Солнечная активность. – М.: Наука, 1983. – 192 с.

Гарвей Д. Атмосфера и океан. – М.: Прогресс. 1982. – 184 с.

Гриббин Дж. Поиск цикличности / Изменения климата. – Л.: Гидрометеоиздат, 1980. – с. 188 – 202.

Дроздов О.А., Васильев Н.В., Раевский А.Н., Смекалова Л.К., Школьный В.П. Климатология. – Л.: Гидрометеоиздат, 1989. – 568 с.

Ермолаев М.М. Введение в физическую географию. – Л.: ЛГУ, 1975. – 250 с.

Зисман Г.А., Тодес О.М. Курс общей физики. – М.: Наука, 1970. – т. III. – 496 с.

Кислов А.В. Климат в прошлом, настоящем и будущем. – М: МАИК «Наука / Интерпериодика», 2001. – 351 с.

Кондратьев К.Я. Лучистая энергия Солнца. – Л.: Гидрометеоиздат, 1954. – 600 с.

Кондратьев К.Я. Актинометрия. – Л.: Гидрометеоиздат, 1965. – 692 с.

Кондратьев К.Я. Глобальный климат и его изменения. – Л.: Наука, 1987. – 232 с.

Кондратьев К.Я., Филипович О.П. Тепловой режим верхних слоев атмосферы. – Л.: Гидрометеоиздат, 1960. – 356 с.

Ландсберг Г.С. (ред). Элементарный учебник физики. – М.: Наука, 1973. – т. 1. – 656 с.

Ландсберг Г.С. (ред). Элементарный учебник физики. – М.: Физматлит, 2000. – т. 1. – 608 с.

Ливингстон У.К. Поток солнечного излучения в системе солнечно-земных связей / Солнечно-земные связи, погода и климата. – М.: Мир, 1982. – с. 61 – 76.

Макарова Е.А., Харитонов А.В., Казачевская Т.В. Поток солнечного излучения. –М.: Наука, 1991. – 400 с.

Миланкович М. Математическая климатология и астрономическая теория колебаний климата. – М.–Л.: ГОНТИ, 1939. – 208 с.

Монин А.С. Введение в теорию климата. – Л.: Гидрометеоиздат, 1982. – 246 с.

Монин А.С., Шишков Ю.А. История климата. – Л.: Гидрометеоиздат, 1979. – 408 с.

Мордвинов A. В. Вариации потока излучения Солнца и энергетика активных областей // Известия РАН, сер. физическая, 1998. – т. 62. – № 6. – c. 1204 – 1205.

Неклюкова Н.П. Общее землеведение. М.: Просвещение, 1976. – 336 с.

Перрен де Бришамбо Ш. Солнечное излучение и радиационный обмен в атмосфере. – М.: Мир, 1966. – 320 с.

Полтараус Б.В., Кислов А.В. Климатология (Палеоклиматология и теория климата). – М.: МГУ, 1986. – 144.

Поток энергии Солнца и его изменения / Ред. О.P. Уайт. – М.: Мир, 1980. – 560 с.

Предстоящие изменения климата. – Л.: Гидрометеоиздат, 1991. – 272 с.

Сивухин Д.В. Общий курс физики. – М.: Физматлит, 2002. – т. 2. – 576 с.

Струве О., Линдс Б., Пилланс Э. Элементарная астрономия. – М.: Наука, 1967. – 468 с.

Фрёлих К. Современные измерения солнечной постоянной / Поток энергии Солнца и его изменения. Ред. О. Уайт. – М.: Мир, 1980. – с. 110 – 127.

Хргиан А.Х. Физика атмосферы. – М.: МГУ, 1986. – 328 с.

Хромов С.П. Метеорология и климатология для географических факультетов. Л.: Гидрометеоиздат, 1968. – 492 с.

Хромов С.П., Петросянц М.А. Метеорология и климатология. – М.: МГУ, 2006. – 582 с.

Эдди Дж. А. Интегральный поток солнечной энергии / Поток энергии Солнца и его изменения. Ред. О. Уайт. – М.: Мир, 1980. – с. 32 – 36.

Эйгенсон М.С. Солнце, погода и климат. – Л.: Гидрометеоиздат, 1963. – 276.

Foukal P.V. Solar astrophysics. – 2nd rev. ed. – Weinheim: Wiley-VCH, 2004. – 480 p.

Lamb H.H. Climate: present, past and future. – London.:, Methuen, 1972. – v. 1. Fundamentals and Climate Now. – 648 p.

Stringer E.T. Foundations of Climatology. Freeman, 1972. – 586 p.